题目内容
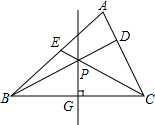 如图,P为△ABC的边BC的垂直平分线上的一点,此垂直平分线交BC于G,且∠PCB=
如图,P为△ABC的边BC的垂直平分线上的一点,此垂直平分线交BC于G,且∠PCB=| 1 |
| 2 |
考点:相似三角形的判定与性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:作BF⊥CE于F点,CM⊥BD于M点.证明Rt△BEF≌Rt△CDM.易证Rt△PBF≌Rt△PCM,得到BF=CM;由于∠A=∠BPE,在四边形ADPE中,根据内角和定理可得∠BEF=∠CDM,所以Rt△BEF≌Rt△CDM.得证.
解答:证明:作BF⊥CE于F点,CM⊥BD于M点,
则∠PFB=∠PMC=90°.
∵PG是BC的垂直平分线,
∴PB=PC.
在△PBF和△PCM中,
,
∴△PBF≌△PCM(AAS),
∴BF=CM;
∵PB=PC,
∴∠PBC=∠PCB=
∠BPE.
∵∠PBC=
∠A,
∴∠A=∠BPE.
∴∠EPD+∠BPE=∠EPD+∠A=180°,
∴∠AEP+∠ADP=180°.
又∠AEP=∠BEF,∠ADP+∠CDM=180°,
∴∠BEF=∠CDM.
在△BEF和△CDM中,
,
∴△BEF≌△CDM(AAS).
∴BE=CD.
则∠PFB=∠PMC=90°.
∵PG是BC的垂直平分线,
∴PB=PC.

在△PBF和△PCM中,
|
∴△PBF≌△PCM(AAS),
∴BF=CM;
∵PB=PC,
∴∠PBC=∠PCB=
| 1 |
| 2 |
∵∠PBC=
| 1 |
| 2 |
∴∠A=∠BPE.
∴∠EPD+∠BPE=∠EPD+∠A=180°,
∴∠AEP+∠ADP=180°.
又∠AEP=∠BEF,∠ADP+∠CDM=180°,
∴∠BEF=∠CDM.
在△BEF和△CDM中,
|
∴△BEF≌△CDM(AAS).
∴BE=CD.
点评:此题考查了线段垂直平分线的性质以及全等三角形的判定与性质.此题难度适中,注意构造全等三角形是关键,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
袋子中装有4个黑球、2个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋子中摸出1个球.下面说法正确的是( )
| A、这个球一定是黑球 |
| B、这个球一定是白球 |
| C、“摸出黑球”的可能性大 |
| D、“摸出黑球”和“摸出白球”的可能性一样大 |
如图图形是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
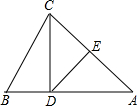 如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD的周长是( )
如图,DE⊥AC,垂足为E,CE=AE.若AB=12cm,BC=10cm,则△BCD的周长是( )| A、22cm | B、16cm |
| C、23cm | D、25cm |
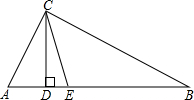 如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )
如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )| A、10° | B、15° |
| C、20° | D、25° |
