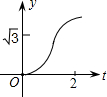题目内容
6.为了解某市20000名考生的毕业会考数学成绩,从中抽出100名考生的数学成绩进行调查,抽出的100名考生的数学成绩是( )| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量..
解答 解:从中抽出100名考生的数学成绩进行调查,抽出的100名考生的数学成绩是样本,
故选:B.
点评 考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.

练习册系列答案
相关题目
17. 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )
 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )| A. | ∠AEB=∠ADC,CD=BE | B. | AC=AB,AD=AE | C. | AC=AB,∠C=∠B | D. | ∠AEB=∠ADC,∠C=∠B |
14.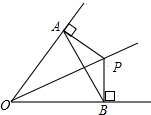 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )| A. | PA=PB | B. | OA=OB | C. | PO平分∠APB | D. | AB垂直平分OP |
1.如图图形经过折叠,能围成正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
18. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )| A. | 30° | B. | 60° | C. | 50° | D. | 40° |
15. 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
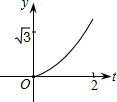
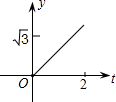
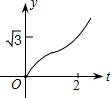
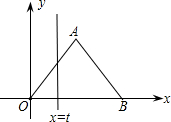 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )