题目内容
8．已知二次函数y=ax2+bx+c的图象与x轴交于（x1，0）、（x2，0）两点，且0＜x1＜1，1＜x2＜2，与y轴交于点（0，-2）．下列结论：①a＜0；②abc＜0；③a+b-2＞0；④2a+b＞1．其中正确结论的个数为（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 由题意画出图象，根据抛物线的开口向下判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解答 解：如图，∵开口方向向上，
∴a＜0，故①正确；
∵0＜x1＜1，1＜x2＜2，
∴-$\frac{b}{2a}$=$\frac{{x}_{1}+{x}_{2}}{2}$＞0，
∴b＞0，
∵c=-2，
∵abc＞0，故②错误；
当x=1时，y＞0，
∴a+b+c＞0，
∵c=-2，
∴a+b-2＞0，故③正确；
∵0＜x1＜1，1＜x2＜2，x1•x2=$\frac{c}{a}$，
∴0＜$\frac{c}{a}$＜2，
∵c=-2，
∴a＜-1，
∴1＜x1+x2＜3，
即1＜x1+x2=-$\frac{b}{a}$＜3，
∴3a+b＜0，a+b＞0，
由3a+b＜0减去a＜-1得：2a+b＜1，故④错误；
∴正确的有①③，
故选B．
点评 考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴和抛物线与坐标轴的交点确定．
练习册系列答案
相关题目
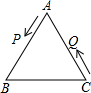如图，在△ABC中，AB=6cm，AC=5cm，点P从A点出发，以2cm/S的速度沿AB方向向B运动，同时点Q从C点出发，以1cm/S的速度沿CA方向向点A运动，当一点到达终止，当一点也停止，连接PQ．设运动时间为ts，当t=$\frac{15}{8}$或$\frac{25}{17}$S时，△ABC与△APQ相似．
16．下列各组线段中，成比例的一组是（ ）
| A． | a=4，b=6，c=5，d=10 | B． | a=2，b=4，c=3，d=6 | ||
| C． | a=2，b=$\sqrt{5}$，c=2$\sqrt{5}$，d=10 | D． | a=0.8，b=3，c=1，d=2 |
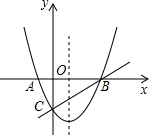如图，二次函数y=x2-2x-3的图象与两坐标轴分别交于A，B，C三点，一次函数的图象与抛物线交于B，C两点．