题目内容
 如图,AC是高为30米的某一建筑,在水塘的对面有一段以BD为坡面的斜坡,小明在A点观察点D的俯角为30°,在A点观察点B的俯角为45°,若坡面BD的坡度为1:
如图,AC是高为30米的某一建筑,在水塘的对面有一段以BD为坡面的斜坡,小明在A点观察点D的俯角为30°,在A点观察点B的俯角为45°,若坡面BD的坡度为1:| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:先延长CB、AD,交于点F,过点D作DE⊥BF,先求出∠ABC和∠AFC的度数,再求出CF和BC、AC的值,然后求出BF,再设DE=x,根据坡面BD的坡度为1:
,得出BE=
x,BD=2x,EF=
x,列出方程,求出x的值,即可得出答案.
| 3 |
| 3 |
| 3 |
解答: 解:延长CB、AD,交于点F,过点D作DE⊥BF,
解:延长CB、AD,交于点F,过点D作DE⊥BF,
∵A点观察点D的俯角为30°,在A点观察点B的俯角为45°,
∴∠ABC=45°,∠AFC=30°,
∴CF=
=
=30
;
BC=AC=30,
∴BF=30
-30,
设DE=x,
∵坡面BD的坡度为1:
,
∴BE=
x,BD=2x,EF=
=
x,
∴
x+
x=30
-30,
解得:x=15-5
,
∴BD=30-10
(米);
故答案为:(30-10
)米.
 解:延长CB、AD,交于点F,过点D作DE⊥BF,
解:延长CB、AD,交于点F,过点D作DE⊥BF,∵A点观察点D的俯角为30°,在A点观察点B的俯角为45°,
∴∠ABC=45°,∠AFC=30°,
∴CF=
| AC |
| tan∠ACF |
| 30 |
| tan30° |
| 3 |
BC=AC=30,
∴BF=30
| 3 |
设DE=x,
∵坡面BD的坡度为1:
| 3 |
∴BE=
| 3 |
| x |
| tan30° |
| 3 |
∴
| 3 |
| 3 |
| 3 |
解得:x=15-5
| 3 |
∴BD=30-10
| 3 |
故答案为:(30-10
| 3 |
点评:本题考查了解直角三角形的应用,用到的知识点是俯角、特殊角的三角函数值、平行线的性质,在解题时要能作出辅助线构造直角三角形.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知甲、乙、丙三数,甲=6+
,乙=2+
,丙=
,则甲、乙、丙的大小关系为( )
| 23 |
| 27 |
| 29 |
| A、甲=乙=丙 |
| B、丙<甲<乙 |
| C、甲<丙<乙 |
| D、丙<乙<甲 |
 如图,经过原点O的抛物线y=ax2-4ax交x轴于点A,顶点B在正比例函数y=2x的图象上.
如图,经过原点O的抛物线y=ax2-4ax交x轴于点A,顶点B在正比例函数y=2x的图象上.
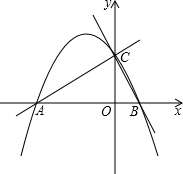 如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,∠CBO的正切值是2.
如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,∠CBO的正切值是2. 小亮在操场沿半圆MABM的路径匀速散步,能近似刻画小亮与出发点M的距离y和散步时间x之间的关系的函数图象是( )
小亮在操场沿半圆MABM的路径匀速散步,能近似刻画小亮与出发点M的距离y和散步时间x之间的关系的函数图象是( )



 如图,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在抛物线y=ax2(a<0)的图象上,则该抛物线的解析式为
如图,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在抛物线y=ax2(a<0)的图象上,则该抛物线的解析式为