题目内容
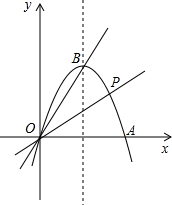
 如图,经过原点O的抛物线y=ax2-4ax交x轴于点A,顶点B在正比例函数y=2x的图象上.
如图,经过原点O的抛物线y=ax2-4ax交x轴于点A,顶点B在正比例函数y=2x的图象上.(1)求抛物线的解析式;
(2)在抛物线上取点P,使得点B关于直线OP对称的对称点B′刚好在x轴上,求点P的坐标;
(3)若点M在直线OB上,点N在x轴上,求PM+MN+PN的最小值.
考点:二次函数综合题
专题:压轴题
分析:(1)把已知函数解析式转化为顶点式,然后根据顶点式解析式来求a的值;
(2)先根据轴对称的性质得到OB=OB′,则点B′的坐标可求,再由中点坐标公式得到BB′的中点C的坐标,运用待定系数法求出直线OC的解析式,与抛物线的解析式联立,即可求出点P的坐标;
(3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,则PM+MN+PN的最小值为线段P′P″的长度,分别求出P′、P″的坐标,运用两点间的距离公式即可求解.
(2)先根据轴对称的性质得到OB=OB′,则点B′的坐标可求,再由中点坐标公式得到BB′的中点C的坐标,运用待定系数法求出直线OC的解析式,与抛物线的解析式联立,即可求出点P的坐标;
(3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,则PM+MN+PN的最小值为线段P′P″的长度,分别求出P′、P″的坐标,运用两点间的距离公式即可求解.
解答: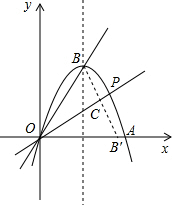
 解:(1)∵y=ax2-4ax=a(x-2)2-4a,
解:(1)∵y=ax2-4ax=a(x-2)2-4a,
∴抛物线y=ax2-4ax的对称轴为:直线x=2,
当x=2时,y=2x=4,
∴顶点B的坐标为:(2,4),
∴-4a=4,
解得:a=-1,
∴抛物线的解析式为:y=-x2+4x;
(2)在抛物线上取点P,使得点B关于直线OP对称的对称点B′刚好在x轴上,设BB′与OP交于点C,则C为BB′的中点.
∵B(2,4),
∴OB=
=2
,
∴OB′=OB=2
,
∴点B′的坐标为:(2
,0),
∴点C(
,
),即C(1+
,2),
则易求直线OC的解析式为:y=
x.
由
,解得
,
(不合题意舍去),
∴点P的坐标为(
,
);
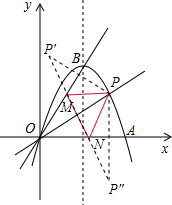 (3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,连接PM,PN,
(3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,连接PM,PN,
此时PM+MN+PN=P′M+MN+P″N=P′P″,值最小.
∵直线OB的解析式为y=2x,PP′⊥OB,
∴设直线PP′的解析式为y=-
x+b,
∵P的坐标为(
,
),
∴-
×
+b=
,
解得b=1+2
,
∴直线PP′的解析式为y=-
x+1+2
.
由
,解得
,
即PP′中点坐标为(
,
),
∴P′点坐标为(
,
),
∵P关于x轴的对称点P″的坐标为(
,
),
∴P′P″=
=
.
即PM+MN+PN的最小值为
.

 解:(1)∵y=ax2-4ax=a(x-2)2-4a,
解:(1)∵y=ax2-4ax=a(x-2)2-4a,∴抛物线y=ax2-4ax的对称轴为:直线x=2,
当x=2时,y=2x=4,
∴顶点B的坐标为:(2,4),
∴-4a=4,
解得:a=-1,
∴抛物线的解析式为:y=-x2+4x;
(2)在抛物线上取点P,使得点B关于直线OP对称的对称点B′刚好在x轴上,设BB′与OP交于点C,则C为BB′的中点.
∵B(2,4),
∴OB=
| 22+42 |
| 5 |
∴OB′=OB=2
| 5 |
∴点B′的坐标为:(2
| 5 |
∴点C(
2+2
| ||
| 2 |
| 4 |
| 2 |
| 5 |
则易求直线OC的解析式为:y=
| ||
| 2 |
由
|
|
|
∴点P的坐标为(
9-
| ||
| 2 |
-7+5
| ||
| 2 |
 (3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,连接PM,PN,
(3)作点P关于OB的对称点P′,关于x轴的对称点P″,连接P′P″,交OB于M,交x轴于N,连接PM,PN,此时PM+MN+PN=P′M+MN+P″N=P′P″,值最小.
∵直线OB的解析式为y=2x,PP′⊥OB,
∴设直线PP′的解析式为y=-
| 1 |
| 2 |
∵P的坐标为(
9-
| ||
| 2 |
-7+5
| ||
| 2 |
∴-
| 1 |
| 2 |
9-
| ||
| 2 |
-7+5
| ||
| 2 |
解得b=1+2
| 5 |
∴直线PP′的解析式为y=-
| 1 |
| 2 |
| 5 |
由
|
|
即PP′中点坐标为(
2+4
| ||
| 5 |
4+8
| ||
| 5 |
∴P′点坐标为(
21
| ||
| 10 |
51+7
| ||
| 10 |
∵P关于x轴的对称点P″的坐标为(
9-
| ||
| 2 |
7-5
| ||
| 2 |
∴P′P″=
(
|
| ||||
| 5 |
即PM+MN+PN的最小值为
| ||||
| 5 |
点评:本题是二次函数综合题,考查了运用待定系数法求二次函数、一次函数的解析式,轴对称的性质,中点坐标公式,两函数交点坐标的求法等知识,综合性较强,有一定难度.运用数形结合、方程思想是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列各函数中,是反比例函数的是( )
| A、y=2x | ||
B、y=
| ||
C、y=
| ||
D、y=
|
如果关于x的方程x2+4x+
+2=0有两个有理根,那么所有满足条件的正整数a的个数是( )
| 10-a |
| A、1 | B、2 | C、3 | D、4 |
 如图,△ABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD与BE交于F,则∠AFB的度数是( )
如图,△ABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD与BE交于F,则∠AFB的度数是( )| A、126° | B、120° |
| C、116° | D、110° |
 已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒.
已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒. 如图,AC是高为30米的某一建筑,在水塘的对面有一段以BD为坡面的斜坡,小明在A点观察点D的俯角为30°,在A点观察点B的俯角为45°,若坡面BD的坡度为1:
如图,AC是高为30米的某一建筑,在水塘的对面有一段以BD为坡面的斜坡,小明在A点观察点D的俯角为30°,在A点观察点B的俯角为45°,若坡面BD的坡度为1: 如图是一个圆形轮子的一部分,请你用直尺和圆规把它补完整.
如图是一个圆形轮子的一部分,请你用直尺和圆规把它补完整.