��Ŀ����
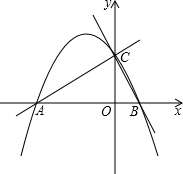 ��ͼ�����κ���y=ax2+2ax+4��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�C����CBO������ֵ��2��
��ͼ�����κ���y=ax2+2ax+4��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�C����CBO������ֵ��2����1����˶��κ����Ľ���ʽ��
��2����ֱ��l����ֱ��AC�غϵ�λ�ó������Ƶ�A˳ʱ����ת����ֱ��AB�غ�ʱ��ֹ�˶���ֱ��l��BC���ڵ�D��P���߶�AD���е㣮
��ֱ��д����P��������·�߳���
�ڵ�D��B��C���غ�ʱ������D��DE��AC�ڵ�E����DF��AB�ڵ�F������PE��PF������ת�����У���EPF�Ĵ�С�Ƿ����仯�������䣬���EPF �Ķ��������仯����˵�����ɣ�
���ڢڵ������£�����EF����EF����Сֵ��
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1������x=0���OC�ij��ȣ������á�CBO����ֵ���OB�ij��ȣ��Ӷ��õ���B�����꣬Ȼ�������κ�������ʽ���a��ֵ�����ɵý⣻
��2�������ù��ɶ�����ʽ���BC�����жϳ���P������·��Ϊ��ABC����λ�ߣ�Ȼ����������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ����
�ڸ���ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�EP=AP=
AD��FP=AP=
AD���ٸ��ݵȱ߶ԵȽǿɵá�CAD=��AEP����BAD=��AFP��Ȼ�����������ε�һ����ǵ������������ڵ������ڽǵĺ������EPF=2��BAC����y=0�������x��һԪ���η��������A�����꣬�Ӷ��õ�OA=OC�������BAC=45�㣬���ɵý⣻
���жϳ���EFP�ǵ���ֱ�������Σ��Ӷ�ȷ��AD��BCʱ��EF��̣����á�ABC�������ʽ���AD��BCʱ��ֵ�������EP��Ȼ����ݵ���ֱ�������ε�б�ߵ���ֱ�DZߵ�
���
��2�������ù��ɶ�����ʽ���BC�����жϳ���P������·��Ϊ��ABC����λ�ߣ�Ȼ����������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ����
�ڸ���ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
���жϳ���EFP�ǵ���ֱ�������Σ��Ӷ�ȷ��AD��BCʱ��EF��̣����á�ABC�������ʽ���AD��BCʱ��ֵ�������EP��Ȼ����ݵ���ֱ�������ε�б�ߵ���ֱ�DZߵ�
| 2 |
����⣺��1����x=0����y=4��
��OC=4��
�ߡ�CBO������ֵ��2��
��
=
=2��
���OB=2��
���B��������2��0����
������κ���y=ax2+2ax+4�ã�4a+2a•2+4=0��
���a=-
��
����κ�������ʽΪy=-
x2-x+4��
��2������Rt��OBC��BC=
=
=2
��
��P���߶�AD���е㣬
���P������·��Ϊ��ABC����λ�ߣ�
������
BC=
��2
=
��
�ڡ�DE��AC��DF��AB��P���߶�AD���е㣬
��EP=AP=
AD��FP=AP=
AD��
���CAD=��AEP����BAD=��AFP��
���EPF=��EPD+��FPD=��CAD+��AEP+��BAD+��AFP=2��CAD+2��BAD=2��BAC��
��y=0����-
x2-x+4=0��
�����ã�x2+2x-8=0��
���x1=2��x2=-4��
���A������-4��0����
��OA=OC=4��
���BAC=45�㣬
���EPF=2��45��=90�㣻
�ۡ�EP=AP=
AD��FP=AP=
AD��
��EP=FP��
�ߡ�EPF=90�㣬
���EFP�ǵ���ֱ�������Σ�
��AD��BCʱ��EF��̣�
��ʱ��S��ABC=
AB•OC=
BC•AD��
��
��|-4-2|��4=
��2
AD��
���AD=
��
��EP=
AD=
��
��EF��С=
EP=
��
=
��
��OC=4��
�ߡ�CBO������ֵ��2��
��
| OC |
| OB |
| 4 |
| OB |
���OB=2��
���B��������2��0����
������κ���y=ax2+2ax+4�ã�4a+2a•2+4=0��
���a=-
| 1 |
| 2 |
����κ�������ʽΪy=-
| 1 |
| 2 |
��2������Rt��OBC��BC=
| OC2+OB2 |
| 42+22 |
| 5 |
��P���߶�AD���е㣬
���P������·��Ϊ��ABC����λ�ߣ�
������
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
�ڡ�DE��AC��DF��AB��P���߶�AD���е㣬
��EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
���CAD=��AEP����BAD=��AFP��
���EPF=��EPD+��FPD=��CAD+��AEP+��BAD+��AFP=2��CAD+2��BAD=2��BAC��
��y=0����-
| 1 |
| 2 |

�����ã�x2+2x-8=0��
���x1=2��x2=-4��
���A������-4��0����
��OA=OC=4��
���BAC=45�㣬
���EPF=2��45��=90�㣻
�ۡ�EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
��EP=FP��
�ߡ�EPF=90�㣬
���EFP�ǵ���ֱ�������Σ�
��AD��BCʱ��EF��̣�
��ʱ��S��ABC=
| 1 |
| 2 |
| 1 |
| 2 |
��
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
���AD=
12
| ||
| 5 |
��EP=
| 1 |
| 2 |
6
| ||
| 5 |
��EF��С=
| 2 |
| 2 |
6
| ||
| 5 |
6
| ||
| 5 |
�����������Ƕ��κ����ۺ����ͣ���Ҫ�����˴���ϵ������������ʽ��������Ǻ����������ε���λ�߶�����ֱ��������б���ϵ����ߵ���б�ߵ�һ������ʣ������ε�һ����ǵ������������ڵ������ڽǵĺ͵����ʣ�����ֱ�������ε��ж������ʣ������ε������Ӧ�ã��ۺ��Խ�ǿ���ѶȽϴ���Ǹ������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
�����Ŀ
 ��ͼ����ABC�У���CAB=52�㣬��ABC=74�㣬AD��BC��BE��AC��AD��BE����F�����AFB�Ķ����ǣ�������
��ͼ����ABC�У���CAB=52�㣬��ABC=74�㣬AD��BC��BE��AC��AD��BE����F�����AFB�Ķ����ǣ�������| A��126�� | B��120�� |
| C��116�� | D��110�� |
�����������������㣨1��2���������е�Ҳ�ڴ˺���ͼ���ϵ��ǣ�������
| A����1��-2�� |
| B����-1��-2�� |
| C����0��-1�� |
| D����-1��-1�� |
 ��֪��Բ�Ľ�Ϊ120�㣬���Ϊ3�е����ξ���һ����Բ��Ͳ��
��֪��Բ�Ľ�Ϊ120�㣬���Ϊ3�е����ξ���һ����Բ��Ͳ�� ��ͼ��AC�Ǹ�Ϊ30��ijһ��������ˮ���Ķ�����һ����BDΪ�����б�£�С����A��۲��D�ĸ���Ϊ30�㣬��A��۲��B�ĸ���Ϊ45�㣬������BD���¶�Ϊ1��
��ͼ��AC�Ǹ�Ϊ30��ijһ��������ˮ���Ķ�����һ����BDΪ�����б�£�С����A��۲��D�ĸ���Ϊ30�㣬��A��۲��B�ĸ���Ϊ45�㣬������BD���¶�Ϊ1�� ��һ�鳤60m����30m�ij����λĵؽ��и��죬Ҫ����������һ��������ȵ����е����м䲿�ֽ���һ�����Ϊ1000m2�ij������̵أ��������е��Ŀ��ȣ�
��һ�鳤60m����30m�ij����λĵؽ��и��죬Ҫ����������һ��������ȵ����е����м䲿�ֽ���һ�����Ϊ1000m2�ij������̵أ��������е��Ŀ��ȣ�