题目内容
已知关于x的一元二次方程mx2-3(m+1)x+2m+3=0.
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当关于x的抛物线y=mx2-3(m+1)x+2m+3与x轴交点的横坐标都是整数,且|x|<4时,求m的整数值.
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当关于x的抛物线y=mx2-3(m+1)x+2m+3与x轴交点的横坐标都是整数,且|x|<4时,求m的整数值.
考点:抛物线与x轴的交点,根的判别式
专题:计算题
分析:(1)由关于x的一元二次方程得到m不为0,根据方程有两个不相等的实数根,得到根的判别式大于0,列出关于m的不等式,求出不等式的解集即可得到m的范围;
(2)对于抛物线解析式,令y=0,表示出x,根据抛物线与x轴交点的横坐标都是整数,根据x的范围即可确定出m的整数值.
(2)对于抛物线解析式,令y=0,表示出x,根据抛物线与x轴交点的横坐标都是整数,根据x的范围即可确定出m的整数值.
解答:解:(1)由题意m≠0,
∵方程有两个不相等的实数根,
∴△>0,即[-3(m+1)]2-4m(2m+3)=(m+3)2>0,
解得:m≠-3,
则m的取值范围为m≠0和m≠-3;
(2)设y=0,则mx2-3(m+1)x+2m+3=0.
∵△=(m+3)2,∴x=
,
∴x1=
,x2=1,
当x1=
是整数时,可得m=1或m=-1或m=3,
∵|x|<4,m=1不合题意舍去,
∴m的值为-1或3.
∵方程有两个不相等的实数根,
∴△>0,即[-3(m+1)]2-4m(2m+3)=(m+3)2>0,
解得:m≠-3,
则m的取值范围为m≠0和m≠-3;
(2)设y=0,则mx2-3(m+1)x+2m+3=0.
∵△=(m+3)2,∴x=
| 3m+3±(m+3) |
| 2m |
∴x1=
| 2m+3 |
| m |
当x1=
| 2m+3 |
| m |
∵|x|<4,m=1不合题意舍去,
∴m的值为-1或3.
点评:此题考查了抛物线与x轴的交点,根的判别式,熟练掌握公式及法则是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目


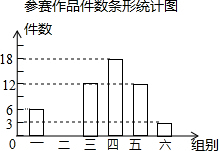 某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答: 已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为
已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为