题目内容
6.将一个底面直径是10厘米、高为36厘米的圆柱锻压成底面直径为20厘米的圆柱,高变成了多少?(1)分析:在锻压过程中,圆柱的体积保持不变,所以这个问题中的等量关系是锻压前的体积=锻压后的体积.
设锻压后圆柱的高为x厘米,则锻压前的体积为(10÷2)2π×36,锻压后的体积为π×(20÷2)2×x;
(2)解:设锻压后圆柱的高为x厘米,根据题意,得方程π×(10÷2)2×36=π×(20÷2)2×x.
解这个方程,得x=9.
所以,锻压后圆柱的高为9厘米.
分析 (1)锻压前的体积=锻压后的体积.
(2)由题意可得锻压前后圆柱的底面半径,高,体积为底面积×高,根据两个圆柱的体积相等可得相关方程,求解即可.
解答 解:(1)在锻压过程中,圆柱的体积保持不变,所以这个问题中的等量关系是:锻压前的体积=锻压后的体积.
锻压前的体积为:(10÷2)2π×36;锻压后的体积为π×(20÷2)2×x;
故答案是:锻压前的体积=锻压后的体积;(10÷2)2π×36;π×(20÷2)2×x;
(2)列出方程为π×(10÷2)2×36=π×(20÷2)2×x,
解得x=9,
所以,锻压后圆柱的高为9厘米.
故答案是:π×(10÷2)2×36=π×(20÷2)2×x.
点评 考查一元一次方程的应用,根据体积相等得到等量关系是解决本题的关键;用到的知识点为:圆柱体的体积=π×底面半径2×高.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
16.下面计算正确的是( )
| A. | (x2)3-2(x3)2=-x12 | B. | (3a2b)2(2ab)3=6a3b2 | C. | (-a4)(-xa)2=-x2a6 | D. | (-xy2)2(xyz)=x3y5 |
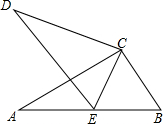 如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.
如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.