题目内容
2．
在⊙O中，AB是⊙O的直径，AB=8cm，$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$，M是AB上一动点，CM+DM的最小值是（ ）| A． | 6cm | B． | 8cm | C． | 10cm | D． | 12cm |
分析 作点C关于AB的对称点C′，连接C′D与AB相交于点M，根据轴对称确定最短路线问题，点M为CM+DM的最小值时的位置，根据垂径定理可得$\widehat{AC}$=$\widehat{AC′}$，然后求出C′D为直径，从而得解．
解答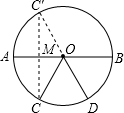 
解：如图，作点C关于AB的对称点C′，连接C′D与AB相交于点M，
此时，点M为CM+DM的最小值时的位置，
由垂径定理，$\widehat{AC}$=$\widehat{AC′}$，
∴$\widehat{BD}$=$\widehat{AC′}$，
∵$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$，AB为直径，
∴C′D为直径，
∴CM+DM的最小值是8cm．
故选B．
点评 本题考查了轴对称确定最短路线问题，垂径定理，熟记定理并作出图形，判断出CM+DM的最小值等于圆的直径的长度是解题的关键．
练习册系列答案
每课必练系列答案
相关题目
17．先化简，再求值（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$）÷$\frac{x}{x-2}$（其中x=3），其计算结果是（ ）
| A． | -$\frac{8}{5}$ | B． | 8 | C． | -8 | D． | $\frac{8}{5}$ |
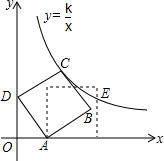如图，在平面直角坐标系中，边长为2的正方形ABCD斜靠在y轴上，点A的坐标为（1，0），反比例函数y=$\frac{k}{x}$图象经过点C，将正方形ABCD绕点A顺时针旋转一定角度后，使得点B恰好落在x轴的正半轴上，此时边BC交反比例图象于点E，则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$．
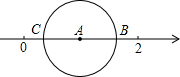如图，数轴上表示1、$\sqrt{2}$的对应点分别为A、B，则以点A为圆心，AB长为半径的圆交数轴于另一点C，则点C表示的数是2-$\sqrt{2}$．