题目内容
8.写出满足x2+4x+M=(3x-8)(x+2)-(x-5)(x+5)的多项式M.分析 把(3x-8)(x+2)-(x-5)(x+5)展开后合并解答即可.
解答 解:(3x-8)(x+2)-(x-5)(x+5)
=3x2-8x+6x-16-x2+25
=2x2-2x+9,
∵x2+4x+M=(3x-8)(x+2)-(x-5)(x+5),
可得M=2x2-2x+9-(x2+4x)
=x2-6x+9.
点评 此题考查多项式的乘法,关键是把(3x-8)(x+2)-(x-5)(x+5)展开计算.

练习册系列答案
相关题目
18.已知函数自变量的取值范围是$\frac{1}{3}$<x≤1,那么这个函数的解析式可能是( )
| A. | y=$\frac{1-x}{\sqrt{3x-1}}$ | B. | y=$\sqrt{\frac{1-x}{3x-1}}$ | C. | y=$\frac{\sqrt{3x-1}}{1-x}$ | D. | y=$\frac{1}{\sqrt{1-x}}$-$\sqrt{3x-1}$ |
 如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.
如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.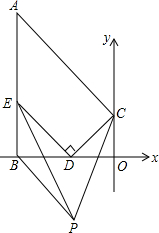 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.