题目内容
4. 如图,∠APC=30°,$\widehat{BD}$=30°,则$\widehat{AC}$=90°,∠AEB=120°.
如图,∠APC=30°,$\widehat{BD}$=30°,则$\widehat{AC}$=90°,∠AEB=120°.
分析 由$\widehat{BD}$=30°,根据弧与圆周角的关系,可求得∠A的度数,然后利用三角形外角的性质,求得∠ADC的度数,即可求得$\widehat{AC}$的度数,再由三角形内角和定理,求得∠AEB的度数.
解答 解:∵$\widehat{BD}$=30°,
∴∠A=$\frac{1}{2}$×30°=15°,
∴∠ADC=∠A+∠APC=15°+30°=45°,
∴$\widehat{AC}$=2×45°=90°,
∵∠ABC=∠ADC=45°,
∴∠AEB=180°-∠A-∠ABC=120°.
故答案为:90°,120°.
点评 此题考查了圆周角定理以及三角形内角和定理.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
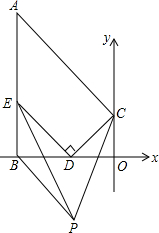 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.