题目内容
17．
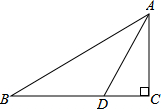如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{5}$-1 | D． | $\sqrt{5}$+1 |
分析 根据∠ADC=2∠B，∠ADC=∠B+∠BAD判断出DB=DA，根据勾股定理求出DC的长，从而求出BC的长．
解答 解：∵∠ADC=2∠B，∠ADC=∠B+∠BAD，
∴∠B=∠DAB，
∴DB=DA=$\sqrt{5}$，
在Rt△ADC中，
DC=$\sqrt{{AD}^{2}-{AC}^{2}}$=$\sqrt{（\sqrt{5}）^{2}-{2}^{2}}$=1；
∴BC=$\sqrt{5}$+1．
故选D．
点评 本题主要考查了勾股定理，同时涉及三角形外角的性质，二者结合，是一道好题．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
7．
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2015秒时，点P的坐标是（ ）
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2015秒时，点P的坐标是（ ）| A． | （2014，0） | B． | （2015，-1） | C． | （2015，1） | D． | （2016，0） |
12．下列长度的三条线段能组成三角形的是（ ）
| A． | 1，2，3 | B． | 1，$\sqrt{2}$，3 | C． | 3，4，8 | D． | 4，5，6 |
9．
某地区共有1800名初三学生，为了解这些学生的体质健康状况，开学之初随机选取部分学生进行体育测试，以下是根据测试成绩绘制的统计图表的一部分．
根据以上信息，解答下列问题：
（1）本次测试学生体质健康成绩为良好的有36人，达到优秀的人数占本次测试总人数的百分比为70%．
（2）本次测试的学生数为200人，其中，体质健康成绩为及格的有18人，不及格的人数占本次测试总人数的百分比为3%．
（3）试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数．
某地区共有1800名初三学生，为了解这些学生的体质健康状况，开学之初随机选取部分学生进行体育测试，以下是根据测试成绩绘制的统计图表的一部分．| 等级 | 测试成绩（分） | 人数 |
| 优秀 | 45≤x≤50 | 140 |
| 良好 | 37.5≤x＜45 | 36 |
| 及格 | 30≤x＜37.5 | |
| 不及格 | x＜30 | 6 |
（1）本次测试学生体质健康成绩为良好的有36人，达到优秀的人数占本次测试总人数的百分比为70%．
（2）本次测试的学生数为200人，其中，体质健康成绩为及格的有18人，不及格的人数占本次测试总人数的百分比为3%．
（3）试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数．
6．有一组数据：1，4，-3，3，4，这组数据的中位数为（ ）
| A． | -3 | B． | 1 | C． | 3 | D． | 4 |