题目内容
2．一枚质地均匀的正方体骰子的六个面分别刻有1到6的点数，将这枚骰子掷两次，其点数之和是7的概率为$\frac{1}{6}$．分析 先画树状图展示所有36种等可能的结果数，再找出点数之和是7的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有36种等可能的结果数，其中点数之和是7的结果数为6，
所以点数之和是7的概率=$\frac{6}{36}$=$\frac{1}{6}$．
故答案为$\frac{1}{6}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
阅读快车系列答案
相关题目
12．
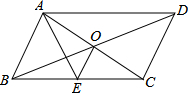如图，?ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①∠CAD=30°；②S?ABCD=AB•AC；③OB=AB；④OE=$\frac{1}{4}$BC，成立的个数有（ ）
如图，?ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①∠CAD=30°；②S?ABCD=AB•AC；③OB=AB；④OE=$\frac{1}{4}$BC，成立的个数有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
13．在如图四个几何体中，主视图与俯视图都是圆的为（ ）
| A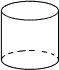． |  | B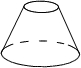． |  | C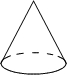． |  | D． |  |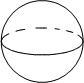
17．
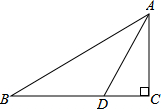如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）
如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{5}$-1 | D． | $\sqrt{5}$+1 |
14．一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
11．某校幵展“文明小卫士”活动，从学生会“督查部”的3名学生（2男1女）中随机选两名进行督导，恰好选中两名男学生的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{4}{9}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{9}$ |