题目内容
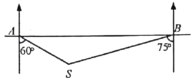
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
【答案】D
【解析】
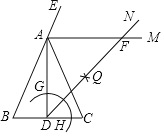
过B作BH⊥AS交AS延长线于H,然后利用直角三角形中特殊角的三角函数求出线段长即可.
解:如图,过B作BH⊥AS交AS延长线于H,

由题意可知∠CAS=60°,∠SBD=75°,∠CAB=∠DBA=90°,AB=30海里
∴∠BAH=30°,∠ABS=15°,
又∵∠AHB=90°,
∴BH=15海里,∠ABH=60°,
∴∠SBH=45°,即△SHB为等腰直角三角形,
∴SH=BH=15海里,
![]() ,
,
∴![]() 海里,
海里,
∴![]() 海里,
海里,
![]() ,
,
![]() 海里,
海里,
故选:D.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目