题目内容
11.已知三角形两边长分别为3和9,则此三角形的第三边的长可能是( )| A. | 4 | B. | 5 | C. | 11 | D. | 15 |
分析 已知三角形的两边长分别为3和9,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.
解答 解:设第三边长为x,则由三角形三边关系定理得9-3<x<9+3,即6<x<12.
因此,本题的第三边应满足6<x<12,把各项代入不等式符合的即为答案.
只有11符合不等式,
故答案为11.
故选C.
点评 此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.-$\frac{1}{3}$的倒数是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
3.3的相反数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -$\frac{1}{3}$ |
20.若反比例函数的图象经过点(3,2),则该反比例函数的解析式是( )
| A. | $y=\frac{2}{3}x$ | B. | $y=\frac{6}{x}$ | C. | $y=\frac{3}{x}$ | D. | y=2x-4 |
1.太阳的半径约为696000千米,将696000用科学记数法表示为( )
| A. | 0.696×106 | B. | 6.96×106 | C. | 69.6×104 | D. | 6.96×105 |
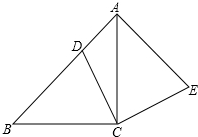 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.