题目内容
6.已知:?ABCD中,DE⊥AB于E交AC于F,且AD=$\frac{1}{2}$FC,求证:∠DAB=3∠ACD.分析 作△DFC的中线DM,先证明∠BAC=∠ACD,∠DAC=∠DMC=2∠ACD,由此即可证明.
解答 证明: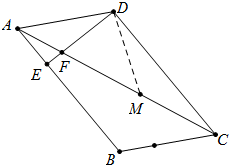 如图作△DFC的中线DM.
如图作△DFC的中线DM.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠ACD,
∵DE⊥AB,
∴DE⊥CD,
∴∠FDC=90°,∵FM=MC,
∴DM=FM=MC=$\frac{1}{2}$FC,
∴∠C=∠MDC,
∵AD=$\frac{1}{2}$FC,
∴AD=DM,
∴∠DAM=∠DMC=∠ACD+MDC=2∠ACD,
∴∠DAB=∠DAC+∠BAC=3∠ACD.
点评 本题考查平行四边形的性质、直角三角形斜边中线定理、等腰三角形的判定和性质等知识,解题的关键是添加辅助线,利用直角三角形斜边中线等于斜边一半解决问题,属于中考常考题型.

练习册系列答案
相关题目
16.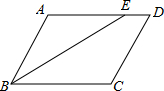 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )| A. | ∠C=120° | B. | AE=6cm | C. | AD=8cm | D. | ∠BED=140° |
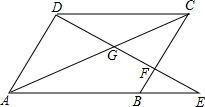 如图,四边形ABCD为平行四边形,试说明:
如图,四边形ABCD为平行四边形,试说明: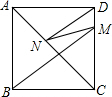 如图,正方形ABCD中,M在DC上,且BM=10,N是AC上一动点,则DN+MN的最小值为10.
如图,正方形ABCD中,M在DC上,且BM=10,N是AC上一动点,则DN+MN的最小值为10.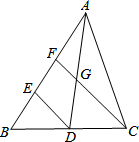 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.
如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.