题目内容
17.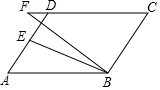 如图,在?ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.
如图,在?ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.
分析 由平行四边形的性质得出AB=CD,AB∥CD,得出∠CFB=∠ABF,由已知得出∠ABF=2∠ABE,证出BE为∠ABF的角平分线,得出∠1=∠2,因此BE交CD的延长线于M,证出∠2=∠3,由AAS证明△ABE≌△DME,得出AB=DM=CD,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠CFB=∠ABF,
又∵∠CFB=2∠ABE,
∴∠ABF=2∠ABE,
∴BE为∠ABF的角平分线,
∴∠1=∠2,
延长BE交CD的延长线于M,如图所示:
∵AB∥CM,
∴∠1=∠3,
∴∠2=∠3,
∴BF=MF,
∵E我AD的中点,
∴AE=DE,
在△ABE和△DME中,$\left\{\begin{array}{l}{∠1=∠3}&{\;}\\{∠AEB=∠DEM}&{\;}\\{AE=DE}&{\;}\end{array}\right.$,
∴△ABE≌△DME(AAS),
∴AB=DM=CD,
∵MF=DM-DF,
∴BF=DC-DF.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质、等腰三角形的判定等知识;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
8. 如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
 如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | B. | $\frac{4π}{3}-2\sqrt{3}$ | C. | $π-\sqrt{3}$ | D. | $\frac{4}{3}π-\sqrt{3}$ |
 (1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)
(1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)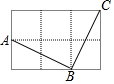 在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.