题目内容
7.设等腰三角形的三条边长分别为a、b、c,已知a=2,b、c是关于x的方程x2-10x+m=0的两个根,求m的值.分析 根据等腰三角形的性质知①方程x2-10x+m=0有一个根为2,将x=2代入可得m的值,再解方程,由三角形三边关系判断是否符合题意;②若b=c,则方程x2-10x+m=0有两个相等的实数根,由根的判别式可得m的值,检验此时方程的根是否符合题意.
解答 解:根据题意知①若b=2或c=2,则方程x2-10x+m=0有一个根为2,
将x=2代入得4-20+m=0,
解得:m=16,
此时方程为x2-10x+16=0,即(x-2)(x-8)=0,
解得:x=2或x=8,
∵2+2<8,不能构成三角形舍去;
若b=c,则方程x2-10x+m=0有两个相等的实数根,
∴(-10)2-4m=0,
解得:m=25,
此时方程为x2-10x+25=0,即(x-5)2=0,
解得:x=5,
∵2+5>5,
可以构成三角形,
故m=25.
点评 本题主要考查等腰三角形的性质、三角形三边的关系、根的判别式及解方程的能力,根据题意分类讨论思想的运用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列说法中不正确的是( )
| A. | 三角形按边分可分为不等边三角形、等腰三角形 | |
| B. | 等腰三角形的内角可能是钝角或直角 | |
| C. | 三角形外角一定是钝角 | |
| D. | 三角形的中线把三角形分成面积相等的两部分 |
2.在数-2,0,4.5,|-9|,-6.79中,属于正数的有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
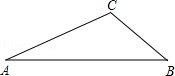 已知△ABC中,∠A=30°,AC=6.
已知△ABC中,∠A=30°,AC=6.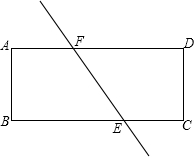 如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.
如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.
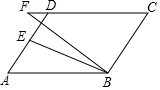 如图,在?ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.
如图,在?ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.