题目内容
5.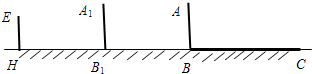 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,其影子长为B1C1;当小明继续走剩下路程的$\frac{1}{3}$到B2处时,其影子长为B2C2;当小明继续走剩下路程的$\frac{1}{4}$到B3处,…,按此规律继续走下去,当小明走剩下路程的$\frac{1}{n+1}$到Bn处时,其影子BnCn的长为$\frac{3}{n+1}$m.(直接用n的代数式表示)
分析 (1)确定灯泡的位置,可以利用光线可逆可以画出;
(2)要求垂直高度GH可以把这个问题转化成相似三角形的问题,图中△ABC∽△GHC由它们对应成比例可以求出GH;
(3)的方法和(2)一样也是利用三角形相似,对应相等成比例可以求出,然后找出规律.
解答 解:(1)如图:形成影子的光线,路灯灯泡所在的位置G.
(2)解:由题意得:△ABC∽△GHC,
∴$\frac{AB}{GH}$=$\frac{BC}{HC}$,
∴$\frac{1.6}{GH}$=$\frac{3}{6+3}$,
解得:GH=4.8(m),
答:路灯灯泡的垂直高度GH是4.8m.
(3)同理△A1B1C1∽△GHC1,
∴$\frac{{A}_{1}{B}_{1}}{GH}$=$\frac{{B}_{1}{C}_{1}}{H{C}_{1}}$,
设B1C1长为x(m),则$\frac{1.6}{4.8}$=$\frac{x}{x+3}$,
解得:x=$\frac{3}{2}$(m),即B1C1=$\frac{3}{2}$(m).
同理$\frac{1.6}{4.8}$=$\frac{{B}_{2}{C}_{2}}{{B}_{2}{C}_{2}+2}$,
解得B2C2=1(m),
∴$\frac{1.6}{4.8}$=$\frac{{B}_{n}{C}_{n}}{{B}_{n}{C}_{n}+\frac{1}{n+1}×6}$,
解得:BnCn=$\frac{3}{n+1}$.
故答案为:$\frac{3}{n+1}$.
点评 本题主要考查相似三角形的应用及中心投影,只要是把实际问题抽象到相似三角形中,利用相似三角形的性质对应边成比例解题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14.若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k,则k的值为( )
| A. | 2 | B. | -1 | C. | 2或-1 | D. | -2或1 |
15.一项工程甲独做需10天完成,乙的工作效率是甲的2倍,两人合作了2天未完成,剩下的工作由乙完成,还需的天数为( )
| A. | 1天 | B. | 2天 | C. | 3天 | D. | 4天 |
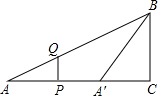 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.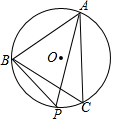 如图,△ABC内接于圆O,∠P=60°,弧$\widehat{BC}$=弧$\widehat{CA}$,则△ABC的特殊形状是等边三角形.
如图,△ABC内接于圆O,∠P=60°,弧$\widehat{BC}$=弧$\widehat{CA}$,则△ABC的特殊形状是等边三角形.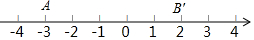 对数轴上的点P进行如下操作:先把点P表示的数乘$\frac{1}{3}$,再把所得数对应的点向右移动1个单位长度,得到点P的对应点P′,点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′,如图,回答下列问题:
对数轴上的点P进行如下操作:先把点P表示的数乘$\frac{1}{3}$,再把所得数对应的点向右移动1个单位长度,得到点P的对应点P′,点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′,如图,回答下列问题: