题目内容
5.若关于x、y的方程组$\left\{\begin{array}{l}{2{x}^{2}+{y}^{2}=2}\\{3x-y=k}\end{array}\right.$有两个相等的实数解.则k的取值范围是±$\sqrt{11}$.分析 由②得y=3x-k ③,把③代入①得:2x2+(3x-k)2=2,根据方程组有两个相等的实数根得出△=(-6k)2-4×11×(k2-2)=-8k2+88=0,解之可得答案.
解答 解:$\left\{\begin{array}{l}{2{x}^{2}+{y}^{2}=2}&{①}\\{3x-y=k}&{②}\end{array}\right.$,
由②得:y=3x-k ③,
把③代入①得:2x2+(3x-k)2=2,
即11x2-6kx+k2-2=0,
∵方程组有两个相等的实数解,
∴△=(-6k)2-4×11×(k2-2)=-8k2+88=0,
解得:k=±$\sqrt{11}$,
故答案为:±$\sqrt{11}$.
点评 本题考查了高次方程:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
(1)表中a的值等于0.25;
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 |
| 摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
| 摸到黑球的频率 $\frac{m}{n}$ | 0.26 | 0.247 | 0.245 | 0.248 | a |
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
13.已知点M(-1,5)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (5,-1) | B. | (-1,-5) | C. | (1,5) | D. | (5,1) |
20. 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )
 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
10.随着手机的普及,微信(一种聊天软件)的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:斤);
(1)根据记录的数据可知前三天共卖出296斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售29斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 鈤 |
| 与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售29斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
 篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:
篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答: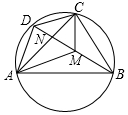 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证: 如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①a>0,b<0;②a-b<0;③a+b>0;④|a|-|b|>0,其中正确的有( )
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①a>0,b<0;②a-b<0;③a+b>0;④|a|-|b|>0,其中正确的有( )