题目内容
9.已知正比例函数y=x与反比例函数y=$\frac{2}{x}$的图象公共点是A,B.点P是x轴负半轴上一点,△ABP的面积是6,求点P的坐标.分析 通过解方程组求出正比例函数y=x与反比例函数y=$\frac{2}{x}$的图象公共点是A,B的交点坐标,再设p(-a,0),由△ABP的面积解方程即可求出结论.
解答 解:根据题意得$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=x}\end{array}\right.$
解得$\left\{\begin{array}{l}{{x}_{1}=\sqrt{2}}\\{{y}_{1=\sqrt{2}}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\sqrt{2}}\\{{y}_{2}=-\sqrt{2}}\end{array}\right.$,
∴A($\sqrt{2}$,$\sqrt{2}$),B(-$\sqrt{2}$,-$\sqrt{2}$),
设p(-a,0),
∵△ABP的面积是6,
∴6=$\frac{1}{2}$×a•$\sqrt{2}$×2,
解得a=3$\sqrt{2}$,
∴求点P的坐标为(-3$\sqrt{2}$,0).
点评 本题主要考查了反比例函数与一次函数的图象,能把解方程组与求图象的交点结合起来是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20.下列各数中无理数的个数是( )
①$\frac{2}{7}$,②$\frac{π}{2}$,③0,④$-\sqrt{6}$,⑤$-0.2\stackrel{•}3\stackrel{•}7$,⑥$\sqrt{9}$.
①$\frac{2}{7}$,②$\frac{π}{2}$,③0,④$-\sqrt{6}$,⑤$-0.2\stackrel{•}3\stackrel{•}7$,⑥$\sqrt{9}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.-$\root{3}{a}=\root{3}{{\frac{4}{5}}}$,则a的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $±\frac{4}{5}$ | D. | $-\frac{64}{125}$ |
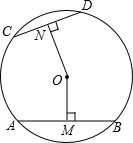 如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由.
如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由.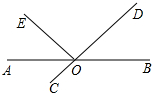 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.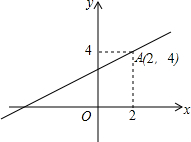 已知函数y=kx+3的图象经过点A(2,4).
已知函数y=kx+3的图象经过点A(2,4).