题目内容
4.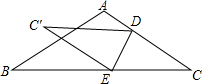 如图,把三角形纸片ABC沿DE折叠,∠ADC′=30°,∠BEC′=40°,求∠C′的度数.
如图,把三角形纸片ABC沿DE折叠,∠ADC′=30°,∠BEC′=40°,求∠C′的度数.
分析 首先由邻补角的定义可知∠C′DC=150°,∠C′EC=140°,然后可求得∠C′+∠C=70°,然后由翻折的性质可知∠C′=∠C,从而求得∠C′的度数.
解答 解:由邻补角的定义可知∠C′DC=180°-∠ADC′=180°-30°=150°,
∠C′EC=180°-∠BEC′=180°-40°=140°.
由四边形的内角和为360°可知;∠C′+∠C=360°-150°-140°=70°,
由翻折的性质可知∠C′=∠C,
∴∠C′=$\frac{1}{2}×70°$=35°.
点评 本题主要考查的是翻折变换、邻补角的定义、四边形的内角和,掌握翻折变换的性质是解题的关键.

练习册系列答案
相关题目
14.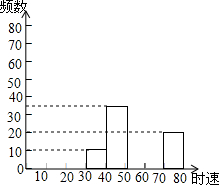 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
| 时速x(km/h) | 频 数 | 频 率 |
| 30≤x≤40 | 10 | 0.05 |
| 40≤x≤50 | 36 | 0.18 |
| 50≤x≤60 | 78 | 0.39 |
| 60≤x≤70 | 56 | 0.28 |
| 70≤x≤80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
9.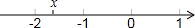 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
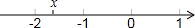 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
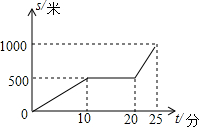 某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系.
某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系.
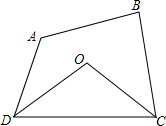 如图,在四边形ABCD中,∠A+∠B=210°,且∠ADC与∠DCB的平分线相交于O,求∠COD的度数.
如图,在四边形ABCD中,∠A+∠B=210°,且∠ADC与∠DCB的平分线相交于O,求∠COD的度数. 如图,已知△ABC中,AD是△ABC外角∠EAC的平分线且交BC的延长线于点D,比较∠ACB与∠B的大小,并说出理由.
如图,已知△ABC中,AD是△ABC外角∠EAC的平分线且交BC的延长线于点D,比较∠ACB与∠B的大小,并说出理由.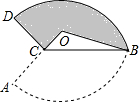 如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.
如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.