题目内容
已知一元二次方程x2+bx-3=0的一根为-3,在二次函数y=x2+bx-3的图象上有三点(-
,y1)、(-
,y2)、(-
,y3),y1、y2、y3的大小关系是( )
| 4 |
| 5 |
| 5 |
| 4 |
| 1 |
| 6 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y1<y3<y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:由条件可求得二次函数的解析式,再根据开口向上的二次函数x距对称轴越近,其对应函数值越小可判断大小关系.
解答:解:
∵一元二次方程x2+bx-3=0的一根为-3,
∴代入可求得b=2,
∴二次函数解析式为y=x2+2x-3,
∴其图象开口向上,对称轴为x=-1,
∴|-1-(-
)|=
,|-1-(-
)|=
,|-1-(-
)|=
,
∵
<
<
,
∴y1<y2<y3,
故选A.
∵一元二次方程x2+bx-3=0的一根为-3,
∴代入可求得b=2,
∴二次函数解析式为y=x2+2x-3,
∴其图象开口向上,对称轴为x=-1,
∴|-1-(-
| 4 |
| 5 |
| 1 |
| 5 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 5 |
| 6 |
∵
| 1 |
| 5 |
| 1 |
| 4 |
| 5 |
| 6 |
∴y1<y2<y3,
故选A.
点评:本题主要考查二次函数的增减性,掌握开口向上的二次函数,当x距对称轴越近其对应的函数值越小是解题的关键.

练习册系列答案
相关题目
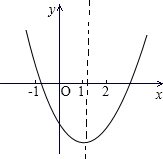 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )| A、M>0,N>0,P>0 |
| B、M<0,N>0,P>0 |
| C、M>0,N<0,P>0 |
| D、M<0,N>0,P<0 |
如图所示的线段或射线,能相交的是( )
A、 |
B、 |
C、 |
D、 |
 如图,AD是∠CAE的平分线,∠B=30°,∠DAE=60°,那么∠ACD等于( )
如图,AD是∠CAE的平分线,∠B=30°,∠DAE=60°,那么∠ACD等于( )| A、90° | B、60° |
| C、80° | D、100° |
 如图,⊙O是△ABC的外接圆AC是⊙O的直径,OD⊥BC于点D.OD=2,则AB的长是( )
如图,⊙O是△ABC的外接圆AC是⊙O的直径,OD⊥BC于点D.OD=2,则AB的长是( )| A、1 | B、2 | C、3 | D、4 |
 如图,△ABC是以圆锥的左视图,若BC=50,cosB=
如图,△ABC是以圆锥的左视图,若BC=50,cosB=| 5 |
| 12 |
| A、1500π | B、3000π |
| C、750π | D、2000π |
等腰三角形的一个角为40°,则它的另外两个角为( )
| A、40°和 100° |
| B、70°和70° |
| C、40°和70° |
| D、40°和 100°或70°和70° |
 从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是
从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是