题目内容
12.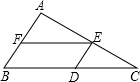 已知如图,△ABC的面积为2400cm2,底边BC长为80cm,若点D在BC边上,E在AC边上,F在AB边上,且四边形BDEF为平行四边形.设BD=xcm,S□BDEF=y cm2.求:
已知如图,△ABC的面积为2400cm2,底边BC长为80cm,若点D在BC边上,E在AC边上,F在AB边上,且四边形BDEF为平行四边形.设BD=xcm,S□BDEF=y cm2.求:(1)y与x的函数关系式;
(2)自变量x的取值范围;
(3)当x取何值时,y有最大值?最大值是多少?
分析 (1)根据△ABC的面积,可求得BC边上的高,易证得△CDE∽△CBA,根据相似三角形得到的比例线段即可用x表示出E到CD的距离,即平行四边形BD边上的高,进而可根据平行四边形的面积计算方法得到y、x的函数关系式.
(2)根据BC的长即可得到x的取值范围.
(3)由(1)得到函数解析式,结合(2)的自变量取值范围,即可根据函数的性质求得y的最大值及对应的x的值.
解答 解:(1)设△DCE的高为hcm,如答图所示,
△ABC的高为bcm,则y=S平行四边形BDEF=x•h;
∵S△ABC=$\frac{1}{2}$BC•b,
∴2400=$\frac{1}{2}$×80b,∴b=60(cm).
∵ED∥AB,∴△EDC∽△ABC.
∴$\frac{h}{b}=\frac{DC}{BC}$,即$\frac{h}{60}=\frac{80-x}{80}$,
∴h=$\frac{3(80-x)}{4}$.
∴y=$\frac{3(80-x)}{4}$•x=-$\frac{3}{4}$x2+60x.
(2)自变量x的取值范围是0<x<80.
(3)∵a=-$\frac{3}{4}$<0,∴y有最大值;
当x=40时,y最大值=1200(cm2).
点评 此题主要考查了相似三角形的判定和性质的知识,关键是根据平行四边形的面积进行分析,能够根据二次函数探求函数的最值,难度适中.

练习册系列答案
相关题目
7.用火柴棒按下图中的方式搭图形.

①按图示规律填空.
②按照这种方式搭下去,搭第n个图形需要4n+1根火柴棒(写最简答案),共有2n个三角形.

①按图示规律填空.
| 图形标号 | (1) | (2) | (3) | (4) |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
| 三角形个数 | 2 | 4 | 6 | 8 |
 如图:已知?ABCD中AE⊥BC于E,AF⊥CD于F,AE=3cm,AF=4cm,CD=8cm,求AD的长.
如图:已知?ABCD中AE⊥BC于E,AF⊥CD于F,AE=3cm,AF=4cm,CD=8cm,求AD的长.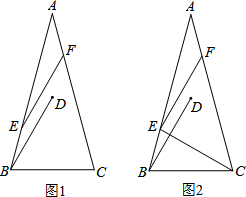 在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.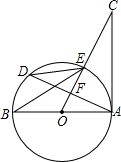 如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$. 如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.求证:AC∥DF.
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.求证:AC∥DF.