题目内容
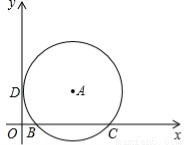
如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A 的坐标是( ).
A.(3,5) B.(4,5) C.(5,3) D.(5,4)
D.
【解析】
试题分析:连接AD,AB,AC,再过点A作AE⊥OC于E,则ODAE是矩形,
∵点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,
∴OB=2,OC=8,BC=6,
∵⊙A与y轴相切于点D,
∴AD⊥OD,
∵由垂径定理可知:BE=EC=3,
∴OE=AD=5,
∴AB=AD=5,
利用勾股定理知AE=4,
∴A(5,4).
故选:D.

考点:1、垂径定理;2、勾股定理.

练习册系列答案
相关题目
(本题满分8分)九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.

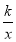 (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则( ).
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则( ).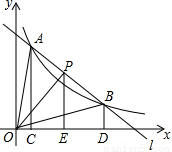
 m;③若直角三角形的两边长为3和4,则第三边的长为 5; ④将抛物线
m;③若直角三角形的两边长为3和4,则第三边的长为 5; ④将抛物线 向左平移2个单位后,得到的抛物线的解析式是
向左平移2个单位后,得到的抛物线的解析式是 ,正确的命题有( ).
,正确的命题有( ).
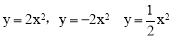 共有的性质是( )
共有的性质是( )