题目内容
某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系。
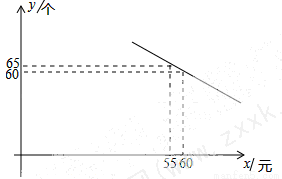
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
(1)y=-x+120.(2)Q=-x2+170x-6000;试销单价定为70元时,该商店可获最大利润,最大利润是1000元.(3)60≤x≤70的整数.
【解析】
试题分析:(1)利用待定系数法将图中点的坐标求出一次函数解析式即可;
(2)根据利润=(售价-成本)×销售量列出函数关系式;
(3)令函数关系式Q≥600,解得x的范围,利用“获利不得高于40%”求得x的最大值,得出销售单价x的范围.
试题解析:(1)设y=kx+b,根据题意得:
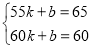
解得:k=-1,b=120.
所求一次函数的表达式为y=-x+120.
(2)利润Q与销售单价x之间的函数关系式为:Q=(x-50)(-x+120)=-x2+170x-6000;
Q=-x2+170x-6000=-(x-85)2+1225;
∵成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.
∴50≤x≤70,
∴当试销单价定为70元时,该商店可获最大利润,最大利润是1000元.
(3)依题意得:-x2+170x-6000≥600,
解得:60≤x≤110,
∵获利不得高于40%,
∴最高价格为50(1+40%)=70,
故60≤x≤70的整数.
考点:1.二次函数的应用;2.一次函数的应用.

 = .
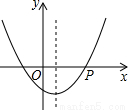
= . 与x轴交于点E .
与x轴交于点E . 
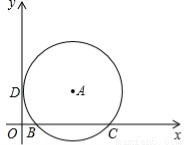
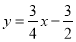 与抛物线
与抛物线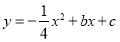 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.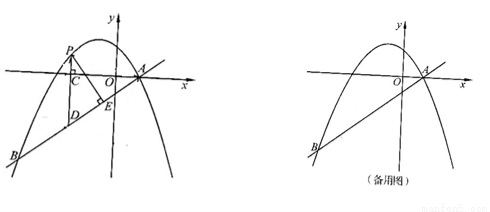
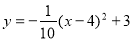 ,由此可知铅球推出的距离是 m.
,由此可知铅球推出的距离是 m.