Question

1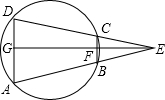．已知：如图，四边形ABCD是圆内接四边形，AB，DC的延长线交于点E，∠AED的平分线分别交BC，AD于点F，G．求证：∠GFC=∠DGF．

Answer 1

分析 由圆内接四边形的性质得出∠ADC=∠EBF，由已知条件和三角形内角和定理证出∠EGD=∠EFB，再有对顶角相等即可得出结论．

解答 证明：∵四边形ABCD是圆内接四边形，
∴∠ADC=∠EBF，
∵EG平分∠AED，
∴∠BEF=∠DEG，
∴∠EGD=∠EFB，
∵∠CFG=∠EFB，∠EGD=∠DGF，
∴∠GFC=∠DGF．

点评 本题考查了圆内接四边形的性质、三角形内角和定理、角平分线以及对顶角相等的性质；熟练掌握圆内接四边形的性质，证出∠EGD=∠EFB是解决问题的关键．