题目内容
11.矩形ABCD中,AB=4,BC=9,点P为BC的三等分点,连接AP,则sin∠PAB=$\frac{3}{5}$或$\frac{{3\sqrt{13}}}{13}$.分析 首先根据题意画出图形,然后由点P为BC的三等分点,分别从BP=$\frac{1}{3}$BC与BP=$\frac{2}{3}$BC,去分析求解即可求得答案.
解答 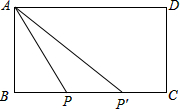 解:如图,∵四边形ABCD是矩形,
解:如图,∵四边形ABCD是矩形,
∴∠B=90°,
∵BC=9,点P为BC的三等分点,
∴BP=$\frac{1}{3}$BC=3或BP′=$\frac{2}{3}$BC=6,
∴AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=5,AP′=$\sqrt{A{B}^{2}+BP{′}^{2}}$=2$\sqrt{13}$,
∴sin∠PAB=$\frac{BP}{AP}$=$\frac{3}{5}$或sin∠P′AB=$\frac{BP′}{AP′}$=$\frac{6}{2\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$.
故答案为:$\frac{3}{5}$或$\frac{{3\sqrt{13}}}{13}$.
点评 此题考查了矩形的性质、勾股定理以及三角函数等知识.注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
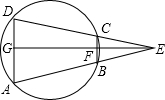 已知:如图,四边形ABCD是圆内接四边形,AB,DC的延长线交于点E,∠AED的平分线分别交BC,AD于点F,G.求证:∠GFC=∠DGF.
已知:如图,四边形ABCD是圆内接四边形,AB,DC的延长线交于点E,∠AED的平分线分别交BC,AD于点F,G.求证:∠GFC=∠DGF.