题目内容
14. 如图,点D、E分别在AB、AC上,且∠ABC=∠AED.若DE=4,AE=5,AB=10,则BC的长为8.
如图,点D、E分别在AB、AC上,且∠ABC=∠AED.若DE=4,AE=5,AB=10,则BC的长为8.
分析 首先由点D、E分别在△ABC的边AB、AC上,且∠AED=∠B可以证明△AED∽△ABC,然后利用相似三角形的性质即可求解.
解答 解:∵点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,
而∠A公共,
∴△AED∽△ABC,
∴AB:AE=BC:DE,
而DE=4,AE=5,AB=10,
∴10:5=BC:4,
∴BC=8.
故答案为:8.
点评 此题主要考查了相似三角形的性质与判定,首先利用有两个对应角相等的两个三角形相似证明三角形相似,然后利用相似三角形的性质问题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目

 如图所示,线段AB=6cm,点C是线段AB上任意一点,点M是线段AC的中点,点N是线段BC的中点,求线段MN的长.
如图所示,线段AB=6cm,点C是线段AB上任意一点,点M是线段AC的中点,点N是线段BC的中点,求线段MN的长.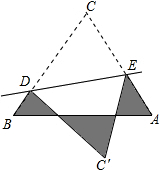 如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm.
如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm.