题目内容
6.已知y=$\sqrt{{x}^{2}-6x+9}+\sqrt{{x}^{2}+2x+1}$,求y的最小值.分析 原式被开方数利用完全平方公式化简,再利用二次根式性质化简,分类讨论x的范围,即可确定出y的最小值.
解答 解:y=$\sqrt{(x-3)^{2}}$+$\sqrt{(x+1)^{2}}$=|x-3|+|x+1|,
当x≤-1时,x-3<0,x+1<0,此时y=3-x-x-1=2-2x,
当x=-1时,y的最小值为4;
当-1≤x≤3时,x+1≥0,x-3≤0,此时y=3-x+x+1=4,
此时y的值恒为4;
当x≥3时,x+1≥0,x-3≥0,此时x-3+x+1=2x-2,
当x=3时,y的最小值为4,
综上,y的最小值为4.
点评 此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.(1)请填写表中的空白处.
(2)观察这一列多项式,写出这一列多项式中的第⑤个多项式x2-5x-6;
(3)写出这一列多项式中的第n个多项式,猜测这个多项式当x=-1时的值,并通过计算说明猜测的结果正确.
| 序号 | 多项式 | 当x=-1时,多项式的值 |
| ① | x2-x-2 | (-1)2-(-1)-2=1+1-2=0 |
| ② | x2-2x-3 | |
| ③ | x2-3x-4 | |
| … | … | … |
(3)写出这一列多项式中的第n个多项式,猜测这个多项式当x=-1时的值,并通过计算说明猜测的结果正确.
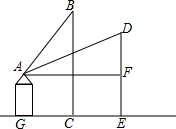 起重机的吊杆与水平线夹角叫倾角,某起重机机身高20米,吊杆倾角是30°时,工作的水平距离AF为10$\sqrt{3}$米,求:当吊杆倾角是60°时,工作的高度BC.
起重机的吊杆与水平线夹角叫倾角,某起重机机身高20米,吊杆倾角是30°时,工作的水平距离AF为10$\sqrt{3}$米,求:当吊杆倾角是60°时,工作的高度BC.