题目内容
10.已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示).
分析 (1)直接利用待定系数法求二次函数解析式即可;
(2)直接利用相似三角形的判定与性质得出对应边的关系进而得出答案.
解答 解:(1)把A(1,0),B(2,0),C(0,-2)分别代入解析式可得:
$\left\{\begin{array}{l}{a+b+c=0}\\{4a+2b+c=0}\\{c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=-2}\end{array}\right.$,
故二次函数的解析式为:y=-x2+3x-2;
(2)当△EDB与△AOC相似时时,有$\frac{AO}{ED}$=$\frac{CO}{BD}$或$\frac{AO}{BD}$=$\frac{CO}{ED}$,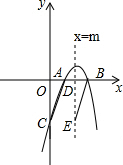
其中AO=1,CO=2,BD=m-2.
①当$\frac{AO}{ED}$=$\frac{CO}{BD}$时,得$\frac{1}{ED}$=$\frac{2}{m-2}$,
解得:ED=$\frac{m-2}{2}$,
∵点E在第四象限,∴E1(m,$\frac{2-m}{2}$).
②当$\frac{AO}{BD}$=$\frac{CO}{ED}$时,得$\frac{1}{2-m}$=$\frac{2}{ED}$,
则∴ED=2m-4.
∵点E在第四象限,∴E2(m,4-2m).
故E1(m,$\frac{2-m}{2}$),E2(m,4-2m).
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质,正确分类讨论是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),(5,0),图象上有三个点(x1,y1),(x2,y2),(x3,y3).若当x1<-1<x2<5<x3时,均有y1y2<0,y2y3<0,则下列说法中正确的是( )
| A. | a<0 | B. | x=2时,y有最大值 | C. | y1y2y3<0 | D. | 5b=4c |
15.以下条件不能判别四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC,∠A=90° | B. | OA=OB=OC=OD | ||
| C. | AB=CD,AB∥CD,AC=BD | D. | AB=CD,AB∥CD,OA=OC,OB=OD |
 如图,在边长为6的等边△ABC中,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是3$\sqrt{3}$.
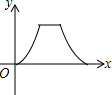
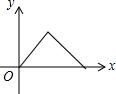
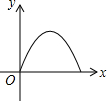
如图,在边长为6的等边△ABC中,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是3$\sqrt{3}$.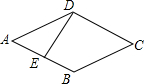 如图,点E是菱形ABCD边上一动点,它沿A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,下列图象中能反映y与x函数关系的是( )
如图,点E是菱形ABCD边上一动点,它沿A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,下列图象中能反映y与x函数关系的是( )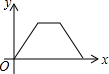
 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为68°.
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为68°.