Question

14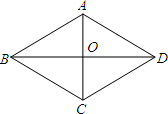．如图，已知菱形ABCD的对角线交于点O，周长是16，BD=2$\sqrt{2}$，求AC．

Answer 1

分析 因为菱形对角线互相垂直平分，故△ABO为直角三角形，根据菱形周长可以计算AB的值，在Rt△ABO中，已知AB，BO，根据勾股定理可以计算AO的长，进而可求出AC的长．

解答 解：∵四边形ABCD是菱形，
∴AC⊥BD，AB=BC=CD=AD，BO=DO，AO=CO，
∵菱形ABCD的周长是16，
∴AB=4，
∵BD=2$\sqrt{2}$，
∴BO=$\sqrt{2}$，
∴AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{14}$，
∴AC=2AO=2$\sqrt{14}$．

点评 本题考查了勾股定理在直角三角形中的运用，考查了菱形对角线互相平分的性质，本题中正确计算AO的长是解题的关键．