题目内容
阅读下列解题过程:请回答下列问题:
(1)
=
=
=
-
=
-2
(2)
=
=
=
-
(1)观察上面的解题过程,请直接写出结果:
=
(2)利用上面信息请化简:
+
+
+…+
的值.
(1)
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
(
|
| 5 |
| 4 |
| 5 |
(2)
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
(
|
| 6 |
| 5 |
(1)观察上面的解题过程,请直接写出结果:
| 1 | ||||
|
(2)利用上面信息请化简:
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
考点:分母有理化
专题:规律型
分析:(1)观察可知,计算结果等于分母有理化因式;
(2)利用分母有理化裂项,然后计算即可得解.
(2)利用分母有理化裂项,然后计算即可得解.
解答:解:(1)原式=
-
.
故答案是:
-
.
(2)原式=
-1+
-
+
-
+…+
-
=
-1.
即
+
+
+…+
=
-1.
| n |
| n-1 |
故答案是:
| n |
| n-1 |
(2)原式=
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
即
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2014 |
点评:本题考查了分母有理化,读懂题目信息,理解分母有理化并把算式写出二次根式的加减的形式是解题的关键.

练习册系列答案
相关题目
下列名人中,①鲁迅、②姚明、③刘徽、④杨利伟、⑤高斯、⑥贝多芬、⑦陈景润、⑧祖冲之.其中是数学家的为( )
| A、①③⑤⑧ | B、③⑤⑦⑧ |
| C、②④⑥⑧ | D、④⑤⑥⑧ |
在1,2,-2这三个数中,任意两数之商的最小值是( )
A、
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
 如图,在△ABC中,N是三条角平分线的交点,EF⊥BN于点N,EF分别交AB、BC于点E、F,∠BAN=20°,∠ENA=30°,则∠FNC=
如图,在△ABC中,N是三条角平分线的交点,EF⊥BN于点N,EF分别交AB、BC于点E、F,∠BAN=20°,∠ENA=30°,则∠FNC= 已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.
已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D. 如图,在Rt△ABC中,∠C=90°,按要求填空:
如图,在Rt△ABC中,∠C=90°,按要求填空: 抛物线y=x2-4x+3
抛物线y=x2-4x+3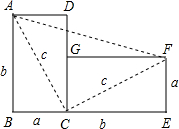 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.