题目内容
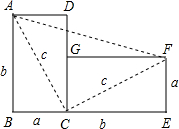 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.考点:勾股定理的证明
专题:
分析:根据S梯形ABEF=S△ABC+S△CEF+S△ACF,利用三角形以及梯形的面积公式即可证明.
解答:证明:∵S梯形ABEF=
(EF+AB)•BE=
(a+b)•(a+b)=
(a+b)2,
∵Rt△CDA≌Rt△CGF,
∴∠ACD=∠CFG,
∵∠CFG+∠GCF=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴S梯形ABEF=
ab+
ab+
c2,
∴
(a+b)2=
ab+
ab+
c2
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵Rt△CDA≌Rt△CGF,
∴∠ACD=∠CFG,
∵∠CFG+∠GCF=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴S梯形ABEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
点评:本题考查了用数形结合来证明勾股定理,证明勾股定理常用的方法是利用面积证明,本题锻炼了同学们的数形结合的思想方法.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4cm2,则S△DEF为( )
已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4cm2,则S△DEF为( )| A、2cm2 | ||
| B、1cm2 | ||
C、
| ||
D、
|
与
最接近的整数是( )
| 40 |
| A、5 | B、6 | C、7 | D、8 |
下列说法中不正确的是( )
| A、函数y=2(x-1)2-1的一次项系数是-4 |
| B、“明天降雨的概率是50%”表示明天有半天都在降雨 |
| C、若a为实数,则|a|<0是不可能事件 |
| D、一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6 |