题目内容
10．在Rt△ABC中，∠C=90°，AC=3，tanA=$\frac{4}{3}$，则AB=5．分析 由于tanA=$\frac{BC}{AC}$=$\frac{4}{3}$，已知AC，即可求得BC的长，由勾股定理可得AB的长．
解答 解：∵在Rt△ABC中，∠C=90°，AC=3，tanA=$\frac{4}{3}$，
∴$\frac{BC}{AC}=\frac{4}{3}$，
∴BC=4，
在Rt△ABC中，AB2=AC2+BC2=32+42=25，
∴AB=5．
故答案为：5．
点评 本题主要考查了解直角三角形，利用勾股定理是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．如果四边形的四边中点所组成四边形是正方形，则下列说法正确的是（ ）
| A． | 原四边形的对角线相等 | B． | 原四边形的对角线互相垂直 | ||
| C． | 原四边形的对角线垂直平分 | D． | 原四边形的对角线互相垂直且相等 |
18．下列命题中，属于真命题的是 （ ）
| A． | 同位角相等 | |
| B． | 多边形的外角和小于内角和 | |
| C． | 面积相等的三角形是全等三角形 | |
| D． | 如果直线l1∥l2，直线l2∥l3，那么ll∥l3 |
5．在Rt△ABC中，∠C=90°，AB=3，AC=2，则cosA的值是（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{5}}{3}$ |
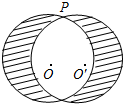如图，点P是⊙O上一点，⊙O的半径为4cm，以点P 为旋转中心，把⊙O逆时针旋转30°得到⊙O′，则图中阴影部分的面积是（$\frac{16}{3}$π+16）cm2．（结果保留π）