题目内容
15.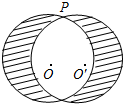 如图,点P是⊙O上一点,⊙O的半径为4cm,以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,则图中阴影部分的面积是($\frac{16}{3}$π+16)cm2.(结果保留π)
如图,点P是⊙O上一点,⊙O的半径为4cm,以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,则图中阴影部分的面积是($\frac{16}{3}$π+16)cm2.(结果保留π)
分析 根据旋转的性质结合菱形的面积求法得出空白面积,进而利用:2(圆的面积-空白面积)=阴影部分的面积求出即可.
解答 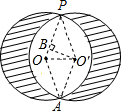 解:如图所示:连接PO,AO,AO′,PO′,过点O′作O′B⊥OP于点B,
解:如图所示:连接PO,AO,AO′,PO′,过点O′作O′B⊥OP于点B,
∵以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,
∴∠OPO′=30°,则∠PO′O=75°,故∠PO′A=150°,
故BO′=$\frac{1}{2}$PO′=2cm,
可得四边形POAO′是菱形,其面积为:PO×O′B=2×4=8(cm2),
故空白面积为:$\frac{150π×{4}^{2}}{360}$-8+$\frac{150π×{4}^{2}}{360}$=($\frac{40}{3}$π-8)cm2,
则图中阴影部分的面积是:2[π×42-($\frac{40}{3}$π-8)]=($\frac{16}{3}$π+16)cm2.
故答案为:($\frac{16}{3}$π+16).
点评 此题主要考查了扇形面积求法以及菱形面积求法等知识,根据题意求出空白面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若反比例函数y=$\frac{2-m}{x}$的图象在第一、第三象限内,则m的取值范围是( )
| A. | m≤2 | B. | m≥2 | C. | m<2 | D. | m>2 |
4.下列说法正确的是( )
| A. | 三点确定一个圆 | B. | 平分弦的直径垂直于弦 | ||
| C. | 等弧所对的圆周角相等 | D. | 垂直于半径的直线是圆的切线 |
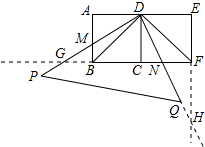 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.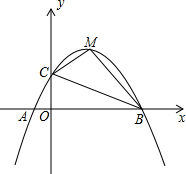 如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(-1,0),B(5,0)两点,与y轴交于点C(0,2)
如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(-1,0),B(5,0)两点,与y轴交于点C(0,2)