题目内容
6. 已知:如图,菱形ABCD的对角线AC和BD相交于点O.求证:菱形ABCD各边中点M,N,P,Q在以O为圆心的同一个圆上.
已知:如图,菱形ABCD的对角线AC和BD相交于点O.求证:菱形ABCD各边中点M,N,P,Q在以O为圆心的同一个圆上.
分析 连接OP,OQ,OM,ON.利用菱形的性质可以证明OP=OQ=OM=ON=$\frac{1}{2}$AB,由此即可证明M,N,P,Q四点在以O为圆心,$\frac{1}{2}$AB为半径的圆上.
解答 解:如图,
连接OP,OQ,OM,ON.
∵四边形ABCD为菱形,
∴AB=BC=CD=DA,且BD⊥AC.
∵M、N、P、Q分别为AB、BC、CD、DA的中点,
∴OP=OQ=OM=ON=$\frac{1}{2}$AB,
∴M,N,P,Q四点在以O为圆心,$\frac{1}{2}$AB为半径的圆上.
点评 此题考查菱形的性质,直角三角形斜边上的中线等于斜边的一半,证明M,N,P,Q在以O为圆心的同一个圆上,只要得出OP=OQ=OM=ON即可.

练习册系列答案
相关题目
14.多项式3a+4b-5c+6中,字母b的系数是( )
| A. | 3 | B. | 4 | C. | -5 | D. | 6 |
11.下列解方程的过程,变形正确的是( )
| A. | 由$\frac{x}{3}-1=\frac{1-x}{2}$,得2x-1=3-3x | |
| B. | 由$\frac{x-2}{2}-\frac{3x-2}{4}=-1$,得2(x-2)-3x-2=-4 | |
| C. | 由$\frac{y+1}{2}=\frac{y}{3}-\frac{3y-1}{6}$-y,得3y+3=2y-3y+1-6y | |
| D. | 由$\frac{x}{4}$+1=$\frac{0.3x+1}{0.1}$+1.2,得$\frac{x}{4}$+1=$\frac{3x+10}{1}$+12 |
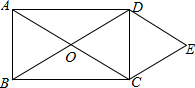 如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.
如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.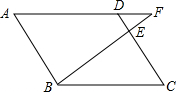 如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$.
如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$. 如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.
如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC. 如图,四边形ADBC中,BC=2BD,AB平分∠DBC,AB=AC,求证:AD⊥BD.
如图,四边形ADBC中,BC=2BD,AB平分∠DBC,AB=AC,求证:AD⊥BD.