题目内容
4．一元二次方程x2-4x+m=0没有实数根，则m应满足的条件是（ ）| A． | m＞4 | B． | m≥4 | C． | m＜4 | D． | m≤4 |
分析 根据方程的系数结合根的判别式即可得出关于m的一元一次不等式，解之即可得出结论．
解答 解：∵方程x2-4x+m=0没有实数根，
∴△=（-4）2-4m=16-4m＜0，
解得：m＞4．
故选A．
点评 本题考查了根的判别式，熟练掌握“当△＜0时，方程无实数根”是解题的关键．
练习册系列答案
相关题目
14．在△ABC和△A1B1C1中，已知∠C=∠A1，∠B=∠B1，要使这两个三角形全等，还需要条件（ ）
| A． | AB=A1B1 | B． | AB=A1C1 | C． | CA=A1C1 | D． | ∠A=∠C1 |
15．已知|m+3|与（n-2）2互为相反数，那么mn等于（ ）
| A． | 6 | B． | -6 | C． | 9 | D． | -9 |
12．下列各说法，正确的是（ ）
| A． | 1的平方根是1 | B． | （-1）2的平方根是±1 | C． | -8是-2的立方根 | D． | 3是$\sqrt{9}$的平方根 |
19．下列叙述，正确的是（ ）
| A． | 两个等腰三角形一定相似 | B． | 两个矩形一定相似 | ||
| C． | 两个菱形一定相似 | D． | 两个正方形一定相似 |
9．当x=-$\frac{1}{2}$时，代数式-2x+10的值等于（ ）
| A． | 9 | B． | -9 | C． | 11 | D． | -11 |
16．
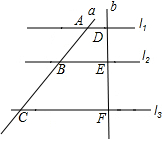如图，直线l1∥l2∥l3，且分别交直线a，b于点A、B、C、D、E、F，若AB=2，BC=3，DE=1，则EF的长为（ ）
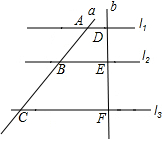如图，直线l1∥l2∥l3，且分别交直线a，b于点A、B、C、D、E、F，若AB=2，BC=3，DE=1，则EF的长为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | 6 | D． | $\frac{1}{6}$ |
13．某款服装按原售价提价a元后，再降价20%，现在售价为b元，则原售价为（ ）
| A． | （$\frac{5}{4}$b+a）元 | B． | （$\frac{5}{4}$b+a）元 | C． | （a+b）元 | D． | （$\frac{5}{4}$a+b）元 |
2．
下列图形中有可能与图相似的是（ ）
下列图形中有可能与图相似的是（ ）| A． |  | B． |  | C． |  | D． |  |