题目内容
20．满足不等式|x-1|+|x+2|＜5的x取值范围是（ ）| A． | -3＜x＜2 | B． | -1＜x＜2 | C． | -2＜x＜1 | D． | -1.5＜x＜3.5 |
分析 根据题目中的不等式，分别讨论x的取值范围把绝对值符号去掉，求出相应的不等式的解集，本题得以解决．
解答 解：|x-1|+|x+2|＜5，
当x≥1时，|x-1|+|x+2|=x-1+x+2=2x+1＜5，解得，x＜2，则1≤x＜2使得|x-1|+|x+2|＜5成立，
当-2≤x＜1时，|x-1|+|x+2|=1-x+x+2=3＜5，则-2≤x＜1使得|x-1|+|x+2|＜5成立，
当x＜-2时，|x-1|+|x+2|=1-x-x-2=-2x-1＜5，得x＞-3，则-3＜x＜-2使得|x-1|+|x+2|＜5成立，
由上可得，足不等式|x-1|+|x+2|＜5的x取值范围是-3＜x＜2，
故选A．
点评 本题考查解一元一次不等式，解答本题的关键是明确解一元一次不等式的方法．
练习册系列答案
相关题目
16．图象经过点（2，3）的反比例函数的解析式是（ ）
| A． | $y=\frac{3}{2x}$ | B． | $y=\frac{2}{3x}$ | C． | $y=\frac{6}{x}$ | D． | $y=\frac{1}{6x}$ |
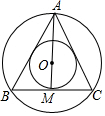如图等边三角形ABC中，AB=6且AM为边BC上的中线，O为重心．求△ABC外接圆的半径及内切圆的半径．