题目内容
9.(1)计算:$\sqrt{4}-(π-3.14)^{0}$-|$\sqrt{3}-2$|+$\frac{1}{\sqrt{3}}$-3tan30°-(-$\frac{1}{2}$)-1;(2)解分式方程:$\frac{x}{x+1}-\frac{x-3}{{x}^{2}-1}$=1.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先把分式方程化为整式方程求出x的值,再代入最减公分母进行检验即可.
解答 解:(1)原式=2-1-(2-$\sqrt{3}$)+$\frac{\sqrt{3}}{3}$-3×$\frac{\sqrt{3}}{3}$+2
=2-1-2+$\sqrt{3}$+$\frac{\sqrt{3}}{3}$-$\sqrt{3}$+2
=1+$\frac{\sqrt{3}}{3}$;
(2)方程两边同时乘以(x+1)(x-1)得,x(x-1)-(x-3)=(x+1)(x-1),
解得x=2,
经检验x=2是原分式方程的根.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质是解答此题的关键.

练习册系列答案
相关题目
 平面直角坐标系中作点A(4,6),B(0,2),C(6,0),并求△ABC的面积.
平面直角坐标系中作点A(4,6),B(0,2),C(6,0),并求△ABC的面积. 如图,菱形ABCD的面积为30cm2,对角线AC的长为12cm,则另一条对角线BD的长等于5cm.
如图,菱形ABCD的面积为30cm2,对角线AC的长为12cm,则另一条对角线BD的长等于5cm.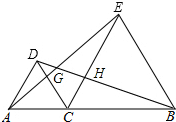 如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.
如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.