��Ŀ����
4���ס�������ͬѧ�ֱ��������0��-$\sqrt{3}$��-1��4�����ſ�Ƭ���������ֲ�ͬ���⣬�����ͬ������Ϸ�����ǽ���Ƭϴ�Ⱥ��������ֵ�һ�泯�·��������ϣ����������ȡһ�ţ�����Ŀ�Ƭ���Żأ����ٴ����µĿ�Ƭ�������ȡһ�ţ���1����ͬѧ�鵽�Ŀ�Ƭ�ϵ��������������ĸ�����$\frac{1}{4}$��
��2�����涨��ͬѧ�鵽��Ƭ�ϵ����ֱ���ͬѧ��ȡ����Ƭ�ϵ����ִ����ͬѧ��ʤ��������ͬѧ��ʤ���������б�������״ͼ������ͬѧ��ʤ�ĸ��ʣ�
���� ��1��������0��-$\sqrt{3}$��-1��4�������������У�-$\sqrt{3}$��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������ͬѧ��ʤ������������ø��ʹ�ʽ������ô𰸣�
��� �⣺��1��������0��-$\sqrt{3}$��-1��4�������������У�-$\sqrt{3}$��
���ͬѧ�鵽�Ŀ�Ƭ�ϵ��������������ĸ����ǣ�$\frac{1}{4}$��
�ʴ�Ϊ��$\frac{1}{4}$��
��2������״ͼ�ã�
�߹���12�ֵȿ��ܵĽ������ͬѧ��ʤ����6�������
����ͬѧ��ʤ�ĸ���Ϊ��$\frac{6}{12}$=$\frac{1}{2}$��
���� ���⿼�����б�������״ͼ������ʣ��õ���֪ʶ��Ϊ������=������������������֮�ȣ�

��ϰ��ϵ�д�
 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
�����Ŀ
14������������ȷ���ǣ�������
| A�� | ��a-b��2=a2-b2 | B�� | ��a+b��2=a2+ab+b2 | C�� | ��1+a����a-1��=a2-1 | D�� | ��a+b����b-a��=a2-b2 |
19������˵����ȷ���ǣ�������
| A�� | Ϊ���˽ⶫ��������ѧ��ÿ������������ʱ�䣬Ӧ�����ղ�ķ�ʽ | |
| B�� | ƽ������ͬ�ļ����������ݣ����������ݵķ���s${\;}_{��}^{2}$=0.03���������ݵķ���s${\;}_{��}^{2}$=0.2�����������ݱȼ��������ȶ� | |
| C�� | ��һö�ʵؾ��ȵ�Ӳ��2�Σ�����1�����泯�� | |
| D�� | ����1��3��4��6��7��8�������5 |
13������3x2-2xy-y2��8x2-3xy+y2�IJ�����ȷ���ǣ�������
| A�� | -2x2-xy-3y2 | B�� | 2x2+xy+3y2 | C�� | -8x2+3xy-y2 | D�� | -5x2+xy-2y2 |
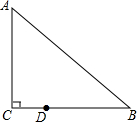 ��ͼ����Rt��ABC�У���C=90�㣬��B=40�㣬��D�ڱ�BC�ϣ�BD=2CD���ѡ�ABC�Ƶ�D��ʱ����תm�Ⱥ�0��m��360���������Bǡ�����ڳ�ʼRt��ABC�ı����ڵ�ֱ���ϣ���ôm=100���120�㣮
��ͼ����Rt��ABC�У���C=90�㣬��B=40�㣬��D�ڱ�BC�ϣ�BD=2CD���ѡ�ABC�Ƶ�D��ʱ����תm�Ⱥ�0��m��360���������Bǡ�����ڳ�ʼRt��ABC�ı����ڵ�ֱ���ϣ���ôm=100���120�㣮