题目内容
18.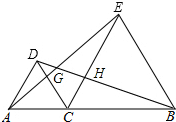 如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.
如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.
分析 先利用旋转的性质得到∠AEC=∠DBC,再利用等边三角形的性质得到CE=CB,∠ACD=∠BCE=60°,则∠DCE=60°,然后利用“ASA”判定△BCH≌△ECG,于是根据三角形全等的性质即可得到结论.
解答 证明:∵△ACE以点C为旋转中心,顺时针旋转60°得到△DCB,
∴∠AEC=∠DBC,
∵△ACD,△ECB都是等边三角形,
∴CE=CB,∠ACD=∠BCE=60°,
∴∠DCE=60°,
在△BCH和△ECG中
$\left\{\begin{array}{l}{CBH=∠CEG}\\{CB=CE}\\{∠BCH=∠ECG}\end{array}\right.$,
∴△BCH≌△ECG,
∴CH=CG.
点评 本题考查了旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
13.计算3x2-2xy-y2与8x2-3xy+y2的差,结果正确的是( )
| A. | -2x2-xy-3y2 | B. | 2x2+xy+3y2 | C. | -8x2+3xy-y2 | D. | -5x2+xy-2y2 |
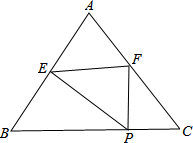 如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.
如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.