题目内容
如图所示,∠BAC=120°,若MP和NQ分别垂直平分A B和AC,求∠PAQ的度数.
B和AC,求∠PAQ的度数.

【考点】线段垂直平分线的性质.
【分析】由MP和NQ分别垂直平分AB和AC,可得PA=PB,AQ=CQ,即可证得∠B=∠BAP,∠C=∠CAQ,又由∠BAC=120°,可求得∠B+∠C的度数,即可得∠BAP+∠CAQ的度数,继而求得答案.
【解答】解:∵PM垂直平分AB,
∴PA=PB,
∴∠B=∠BAP,
同理:QC=QA,
∴∠C=∠CAQ,
∵∠BAC=120°,
∴∠B+∠C=60°,
∴∠BAP+∠CAQ=60°,
∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=60°.
【点评】此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意求得∠BAP+∠CAQ的度数是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 x+1;④y=(
x+1;④y=( ﹣
﹣ )x.
)x.


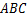 中,若三边长分别为9,12,15,则以两个这样的三角形拼成的长方形的面积为__________.
中,若三边长分别为9,12,15,则以两个这样的三角形拼成的长方形的面积为__________.