Question

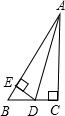
如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于(     )

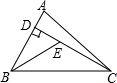
A．10     B．7       C．5       D．4

Answer 1

C【考点】角平分线的性质．

【分析】作EF⊥BC于F，根据角平分线的性质求得EF=DE=2，然后根据三角形面积公式求得即可．

【解答】解：作EF⊥BC于F，

∵BE平分∠ABC，ED⊥AB，EF⊥BC，

∴EF=DE=2，

∴S_△BCE=BC•EF=×5×2=5，

故选C．

【点评】本题考查了角的平分线的性质以及三角形的面积，作出辅助线求得三角形的高是解题的关键．