Question

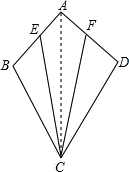
如图，在一个风筝ABCD中，AB=AD，BC=DC，分别在AB、AD的中点E、F处挂两根彩线EC、FC．求证：EC=FC．

Answer 1

【考点】全等三角形的应用．

【专题】证明题．

【分析】连接AC，先利用SSS证明△ABC≌△ADC，根据全等三角形的对应角相等得出∠1=∠2，再利用SAS证明△EAC≌△FAC，即可得到EC=FC．

【解答】证明：如图，连结AC．

在△ABC与△ADC中，

，

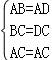∴△ABC≌△ADC（SSS），

∴∠EAC=∠FAC．

∵E、F分别是AB、AD的中点，

∴AE=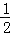AB，AF=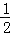AD，

∵AB=AD，

∴AE=AF．

在△AEC与△AFC中，

，

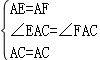∴△AEC≌△AFC（SAS），

∴EC=FC．

【点评】本题主要考查全等三角形的判定与性质及学生对规律的探索能力，难度适中．本题通过作出辅助线，构造三角形全等的条件，判定三角形全等，从而利用三角形全等的性质得到边相等．