题目内容
如图,在直角梯形纸片ABCD中,AB∥DC,∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.连接EF并展开纸片.
(1)判断四边形ADEF的形状,并说明理由.
(2)取线段AF的中点G,连接EG、DG,如果DG∥CB,试说明四边形GBCE是等腰梯形.

解:(1)四边形ADEF为正方形.理由如下:
∵纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF,
∴∠DEF=∠A=90°,DA=DE,
∵AB∥DC,
∴ ∠ADE=90°,
∠ADE=90°,
∴四边形ADEF为矩形,
而DA=DE,
∴四边形ADEF为正方形;
(2)∵DG∥CB,DC∥AB,
∴四边形BGDC是平行四边形,
∴BC=DG,DC=BG,
∴EC≠BG,
∴四边形EGBC是梯形,
又∵G点为AF的中点,
∴AG=GF,
而正方形ADEF为轴对称图形,
∴GE=DG,
∴EG=CB,
∴四边形EGBC为等腰梯形.

练习册系列答案
相关题目

 BE,则长AD与宽AB的比值是 .
BE,则长AD与宽AB的比值是 .
 ),一次函数y=kx+b的图象过A、B两点.
),一次函数y=kx+b的图象过A、B两点. (m>0)的图象上,求反比例函数的表达式.
(m>0)的图象上,求反比例函数的表达式.
 ,则DF的长等于( )
,则DF的长等于( )
 B.
B. C.
C. D. 2
D. 2
 将线段
将线段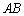 放在每个小正方形的边长为
放在每个小正方形的边长为 的网格中,点
的网格中,点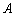 ,点
,点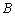 均落在格点上.
均落在格点上. ,使
,使 ,并简要说明画图方法(不要求证明) .
,并简要说明画图方法(不要求证明) .