题目内容
2.分解因式:①25(m+n)2-(m-n)2
②x2+y2+2xy-1.
分析 ①原式利用平方差公式分解即可;
②原式前三项利用完全平方公式分解,再利用平方差公式分解即可.
解答 解:①原式=[5(m+n)+(m-n)][5(m+n)-(m-n)]=(6m+4n)(4m+6n)=4(3m+2n)(2m+3n);
②原式=(x+y)2-1=(x+y+1)(x+y-1).
点评 此题考查了提公因式法与公式法的综合运用,以及因式分解-分组分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
13.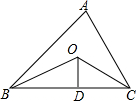 如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
 如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
10.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
14.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差1的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
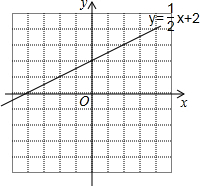 探究问题.
探究问题. 在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M.
在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M. 已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.
已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.