题目内容
20.如图1,有甲乙两个圆柱形水槽,其中乙水槽内装有一定量的水,甲水槽内没有装水,且甲水槽中放有两个完全相同且底面为正方形的长方形铁块.现将乙水槽内的水匀速注入甲水槽中,两个水槽内的水深y(cm)与注水时间x(s)的函数关系如图2所示,根据图象解答下列问题:
(1)线段DE表示乙水槽内的水深与注水之间的函数关系(填“甲”或“乙”).
(2)由A点的坐标可知长方体铁块的底面边长为5cm,并结合B点的坐标可知长方体铁块的高为9cm,所以一个长方体的体积为225cm3;
(3)若设注水速度为v cm3/s,甲水槽的底面积为S,
①求注水前乙水槽内装有水多少cm3?
②求线段BC对应的函数表达式.
分析 (1)结合图象,可知只有乙槽水位是匀速下降的,从而得出结论;
(2)结合图1甲槽以及图2中A、B两点的纵坐标,可以得出长方体铁块的底面边长及高,结合长方体体积公式即可得出结论;
(3)①由存水量=流速×时间可以得出结论;
②根据上升高度=$\frac{流速}{底面积}$可得出线段BC斜率,根据B点坐标即可得出线段BC的解析式.
解答 解:(1)线段DE表示水位匀速下降,所以应该表示的为乙水槽内的水深与注水之间的函数关系.
故答案为:乙.
(2)观察图1甲槽与图2两次转折点A、B,可知:
长方体铁块的底面边长为5cm,高为9cm,
则长方体体积V=5×5×9=225cm3.
故答案为:5;9;225.
(3)①∵注水速度为v cm3/s,乙水槽倒完水的时间为40秒,
∴乙水槽存水量=40v,
故注水前乙水槽内装有水40vcm3.
②线段BC段水面上升的速度为$\frac{v}{S}$,故设BC段的解析式为y=$\frac{v}{S}$x+b,
∵点B(30,14)在线段BC上,
∴有14=$\frac{v}{S}$×30+b,解得:b=$\frac{14S-30v}{S}$,
故线段BC对应的函数表达式y=$\frac{v}{S}$x+$\frac{14S-30v}{S}$=$\frac{v}{S}$(x-30)+14(30≤x≤40).
点评 本题考查了一次函数的图象、长方体的体积公式以及待定系数法求函数解析式,解题的关键是:数形结合解决问题.本题属于基础题型,难度不大,(1)(3)难度不大,(2)由于图形不标准造成干扰,只能由多审题得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某商品两次价格下调后,单价从5元变为4.05元,则平均调价的百分率为( )
| A. | 9% | B. | 10% | C. | 11% | D. | 12% |
9.下列方程是一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-2x=x2+1 | C. | 4x2-9=(2x-1)2 | D. | x2-1=0 |
10.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
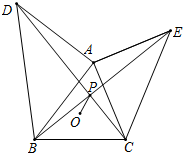 如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$.
如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$. 探究问题.
探究问题.