题目内容
14.计算:$\frac{{1}^{2}-{2}^{2}}{1+2}$+$\frac{{3}^{2}-{4}^{2}}{3+4}$+$\frac{{5}^{2}-{6}^{2}}{5+6}$+…+$\frac{201{5}^{2}-201{6}^{2}}{2015+2016}$.分析 认真审题,利用平方差公式将分子写成两个因数的乘积的形式,再约分,据此即可得到本题的答案.
解答 解:原式=$\frac{(1-2)(1+2)}{1+2}+\frac{(3-4)(3+4)}{3+4}+\frac{(5-6)(5+6)}{5+6}+$…+$\frac{(2015-2016)(2015+2016)}{2015+2016}$
=(-1)+(-1)+(-1)+…+(-1)
=-1008.
点评 本题主要考查了利用因式分解简化运算的问题,因式分解的一般步骤为:有公因式的先提取公因式,没有公因式的考虑运用公式法,分解因式必须分解到每一步都不能再分解为止.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
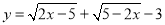 ,求2xy的值.
,求2xy的值.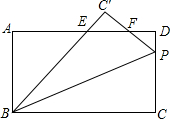 如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.
如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.