题目内容
19.已知实数a满足a2+$\frac{1}{{a}^{2}}$-3a-$\frac{3}{a}$=8,求a+$\frac{1}{a}$的值.解:a2+$\frac{1}{{a}^{2}}$-3a-$\frac{3}{a}$-8=0.
a2+2•a•$\frac{1}{a}$+($\frac{1}{a}$)2-3(a+$\frac{1}{a}$)-10=0.
∴(a+$\frac{1}{a}$)2-3(a+$\frac{1}{a}$)-10=0.
∴a+$\frac{1}{a}$=5,或a+$\frac{1}{a}$=-2.
分析 利用配方法将已知方程转化为关于(a+$\frac{1}{a}$)的方程,然后利用因式分解法解方程即可.
解答 解:a2+$\frac{1}{{a}^{2}}$-3a-$\frac{3}{a}$-8=0.
a2+2•a•$\frac{1}{a}$+($\frac{1}{a}$)2-3(a+$\frac{1}{a}$)-10=0.
∴( a+$\frac{1}{a}$)2-3(a+$\frac{1}{a}$)-10=0.
∴( a+$\frac{1}{a}$-5)( a+$\frac{1}{a}$+2)=0
∴a+$\frac{1}{a}$=5,或a+$\frac{1}{a}$=-2.
故答案是:a+$\frac{1}{a}$;5;-2.
点评 本题考查了换元法解分式方程.将已知方程转化为以 (a+$\frac{1}{a}$)为未知数的一元二次方程是解题的难点.

练习册系列答案
相关题目
 如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.
如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.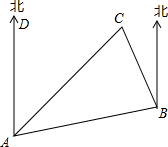 如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.